| Reference: | Yakov Ben-Haim |
| Opening paragraph | This document addresses the following Frequently Asked Questions about info-gap decision theory. This document is not a comprehensive presentation of info-gap theory, but does contain references to some literature. Many more literature citations are found at: http://www.technion.ac.il/yakov/IGT/igt.htm |
| Scores | TUIGF:100% SNHNSNDN:100% GIGO:100% |
A number of info-gap adherents have indicated to me that, as far as they are concerned, in this document Yakov Ben-Haim responds to my criticism of info-gap decision theory. Therefore, as things stand, info-gap decision theory is not debunked --- as I claim --- but is merely "controversial". The controversy, so they tell me, is due to the different opinions of two scholars on info-gap decision theory: Yakov Ben Haim --- the Father of this theory --- and yours truly, the person who claims that this theory is without any merit.
So, in this review I shall put in writing what I tell those who seem to prefer the "safe haven" of a supposed "controversy" about info-gap decision theory, rather than come down one way or the other, to declare unequivocally which position is the correct one. I shall address each FAQs and comment on it. Whenever necessary I shall also explain in detail the errors in Ben-Haim's claims.
However, ...
I do not intend to duplicate here in full what I have already published elsewhere. So if you take this business seriously, I suggest that you read the following articles, where I formally and rigorously debunk info-gap decision theory:Sniedovich, M. (2010) A bird's view of info-gap decision theory. Journal of Risk Fianance, 11(3), 268-283.Sniedovich, M. (2011) Black Swans, new Nostradumouses, voodoo decision theories, and the science of decision maling in the face of severe uncertainty, International Transactions in Operational Research, preview on line.
I should point out that my first article outlining my critique of info-gap decision theory dates back to 2007:
Sniedovich, M. (2007) The art and science of modeling decision-making under severe uncertainty, Decision Making in Manufacturing and Services, 1-2, 111-136 (Free PDF File).
And, before I take up the specific FAQs, I want to point out the following.
Info-gap decision theory is not in any way, shape, or form, "controversial". It is not "controversial" for the simple reason that there is nothing about it that is subject to controversy.To be precise, everything about info-gap decision theory is crystal clear. The hard facts stating exactly what info-gap decision theory is are clear cut and there for all to see. These facts are spelled out by three simple, crystal clear theorems.
This means that, short of these theorems being disproved, the facts established by these theorems are incontrovertible, much less are they open to debate.
In a word, there is no controversy regarding what info-gap decision theory is because there is nothing to argue about.
The three theorems are as follows:
- The Maximin Theorem states that info-gap's generic model is a simple instance of Wald's famous maximin model (circa 1940) (see proof).
- The Radius of Stability Theorem states that info-gap's generic model is that simple instance of Wald's maximin model that is known universally as the Radius of stability model (see proof) .
- The Invariance Theorem states that info-gap's robustness analysis is afflicted by a No Man's Land Syndrom. That is, vast regions of the uncertainty space may have no impact whatsover on the results of the robustness analysis (see proofs in the two articles cited above).
The point is then that my claims regarding the flaws in info-gap decision theory are not just "opinions" or "views" that, as it were, are on a par with, but different from, other "opinions" or "views", so that one can tend towards this view rather than the other. All my claims depicting info-gap decision theory are substantiated by rigorous, formal arguments that whenever necessary are backed up by rigorous formal proofs. Hence, to reject my depiction of info-gap decision theory one has to provide a rigorous formal argument disproving these proofs.
public-domain.zorger.com Hence, info-gap adherents who are sitting on the fence "undecided", maintaining that info-gap decision theory is "merely controversial", must decide which way to jump. Because, the discussion about info-gap decision theory is not about some grand, ambiguous ideas that can be interpreted in various, even contradictory ways.
All we are talking here about is a very small set of extremely simple axioms and simple, concrete mathematical models based on these axioms.
Therefore, the onus is on analysts who claim that info-gap decision theory is "controversial" to declare unequivocally which position stipulating the nature of these models, their mode of operation, their capabilities and their scope, is -- in their opinion -- the correct one.
Now, some basic non-controversial details.
This entire discussion is about two very simple mathematical models, namely info-gap's robustness model and info-gap's decision model (for robustness). These models have the following generic formats:
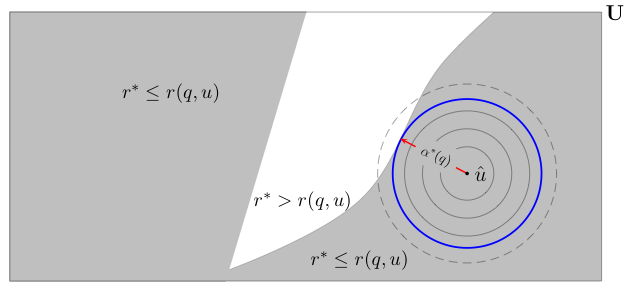
Info-gap's robustness model: α*(q):= max {α≥0: r* ≤ r(q,u),∀u∈U(α,û)} , q∈Q Info-gap's decision model:
α*:= max α*(q) q∈Q = max max {α≥0: r* ≤ r(q,u),∀u∈U(α,û)} q∈Q where
- Q = set of decisions available to the decision maker.
- u = parameter whose true value is unknown, indeed is subject to severe uncertainty.
- û = estimate of the true value of u.
- U(α,û) = ball of radius α around û.
- r(q,u) = performance level of decision q given u.
- r* = critical performance level.
Let U denote the smallest set containing all the balls U(α,û), α≥0. We shall refer to U as the uncertainty space.
In words, the robustness of decision q, denoted by α*(q), is the radius of the largest ball U(α,û) around the estimate û, all of whose elements satisfy the performance requirement r* ≤ r(q,u).
The following picture illustrates the definition of robustness according to info-gap decision theory:
The uncertainty space (U) is represented by the large rectangle. The shaded area represents the subset of U whose elements satisfice the performance requirement associated with decision q. We shall refer to this area as the region of stability associated with decision q.
The robustness of decision q is equal to the radius of the bold blue circle that is tangent to the boundary of the region of stability, but does not cross it. It is the radius of the largest circle all of whose elements are in the region of stability of decision q.
Unsurprisingly, local robustness of this type is known universally as Radius of Stability (circa 1960). But, info-gap adherents are unaware of this fact.
Thus, pursuant to the robustness determined by info-gap's robustness model, decisions are ranked according to their robustness: the larger the robustness, the better the decision. Hence, the optimal decision is that whose robustness is the largest.
And in this connection, there are only two relevant axioms to consider, namely
- Contraction: U(0,û) = {û}.
- Nesting: U(α,û) ⊆ U(α+ε,û) , ∀α,ε≥0.
This is all you need to know about info-gap decision theory to be able to determine that it is fundamentally flawed.
Consider now my claim that this model is a simple instance of Wald's maximin model (circa 1940) --- more specifically, that simple instance which is known universally as Radius of Stability model (circa 1960). To support this claim, I set out a formal rigorous proof.
"Undecided" info-gap adherents can easily verify the validity of this proof.
If they judge the proof valid, then they cannot maintain that this claim is controversial. If they find the proof to be invalid, then they must justify their claim formally indicating where exactly did the proof go wrong.
Those who are unable to verify the proof, should admit to it and excuse themselves from the discussion, as they are in no position to make any pronouncements on this matter.
I demand no less from myself. To show that a particular claim made in the info-gap literature is incorrect/wrong or what have you, I specify exaclty why this is so, and I identify the flaws/errors in the arguments supporting the claim.
That said, I should point out that info-gap's robustness model is extremely simple. So, identifying and explaining the flaws in the numerous unfounded, erroneous claims about this model, circulating in the info-gap literature, is elementary. I note this fact to make the point that one need not be a trained mathematician to comprehend why info-gap decision theory is fundamentally flawed.
If you suspect that not everything in the ensuing discussion may be of interest to you, but you would nevertheless want to learn about the main drift of my position, you can go directly to: Official Mobile Debunker of info-gap decision theory.
The FAQs
The FAQS covered in the document under consideration in this review are these:
- Does an Info-Gap Model only Deal with Local Uncertainty?
- Are Info-Gap Models of Uncertainty Based on the Principle of Ignorance?
- Is Robust-Satisficing the Same as Max-Min?
- Can the Max-Min Strategy be Used to Describe Robust-Satisficing Behavior?
- Does Maximum Robustness Imply Maximum Likelihood of Success?
- Can Max-Min Computational Tools be Used for Info-Gap Robustness?
- Can Info-Gap Theory Deal with Multiple Performance Requirements?
At this stage I shall only quote Ben-Haim's formulation of the specific FAQs and I shall comment on them. At a later stage I shall expand this commentary by responding to Ben-Haim's specific answer to each FAQ on his list. Of particular importance to this discussions are FAQ 1, FAQ 3, FAQ 4, and FAQ 5.
FAQ 1: Does an Info-Gap Model only Deal with Local Uncertainty?
Ben-Haim widens the scope of this question by breaking it down into the following sub-questions:
Question: The best estimate, û, of an info-gap model of uncertainty is sometimes a wild guess, since in most cases the horizon of uncertainty, α, is unknown. How sure can we be that an info-gap model of uncertainty U(α,û) is not just a local analysis of risks which grossly errs in the true value u? Is it not preferable to employ qualitative methods for managing "unknown-unknowns"? Does the info-gap approach simply sweep major risks under the carpet?
Take special note of the sub-question
Is it not preferable to employ qualitative methods for managing "unknown-unknowns"?
The mind boggles at the implicit suggestion that the choice one has here is between "info-gap decision theory" and "qualitative" methods. My point of course is that this sub-question gives the impression that info-gap decision theory is the only "quantitative" theory in town capable of dealing with non-probabilistic, severe uncertainty.
Obviously, all one can say about this leading question is that what is being swept under the carpet, in the first place, is the facts about available quantitative methods for dealing with a non-probabilisitc quantification of severe uncertainty. Which means, of course, that the question that ought to have been asked is this:
How does info-gap decision theory compare with methods/theories offered by decision theory and robustness optimization for the treatment of a non-probabilistic severe uncertainty?
That said, my short answer to this question is this:
Moshe's Answer:
- Info-gap's robustness model is a simple instance of a model of local robustness known universally as radius of stability model (circa 1960).
- This means that info-gap's robustness model is, by definition, a model of local robustness. That is, info-gap's robustness analysis seeks decisions that are robust against small perturbations in the estimate û, to the total exclusion of the performance of the decisions in the rest of the uncertainty space.
- Given this inherently local mode of operation, info-gap's robustness model is utterly unsuitable for the treatent of severe uncertainty of the type that info-gap decision theory claims to take on.
- The inevitable conclusion, therefore, is that info-gap's robustness model does indeed sweep major risks under the carpet: it does not seek robustness against severe uncertainty, it seeks robustness against small perturbations in the estimate.
To better appreciate why info-gap's robustness model does nothing else but "sweep major risks under the carpet", keep in mind that the radius of stability model was devised expressly for the purpose of quantifying, analyzing and managing small perturbations in the nominal value of the parameter of interest. This means that radius of stability models are ill-equipped to handle severe uncertainty that is characterized by
- A vast uncertainty space (often unbounded)
- A poor estimate (a guess, sometimes just a wild guess)
- A likelihood-free quantification of uncertainty.
But this is precisely the type of uncertainty that info-gap decision theory is supposed to deal with!
I should point out that info-gap decision theory has the dubious distinction of being the only decision theory to propose the use of a radius of stability model for the treatment of severe uncertainty of this type.
That is, info-gap decision theory is the only decision theory to contend that a radius of stability analysis (read: a local analysis) conducted in the neighborhood of a wild guess provides a reliable recipe for identifying decisions that are robust against severe uncertainty in the true value of the parameter of interest.
To makes vivid the implications of this absurd proposition, consider the following picture:
Radius of Stability of decision q' | 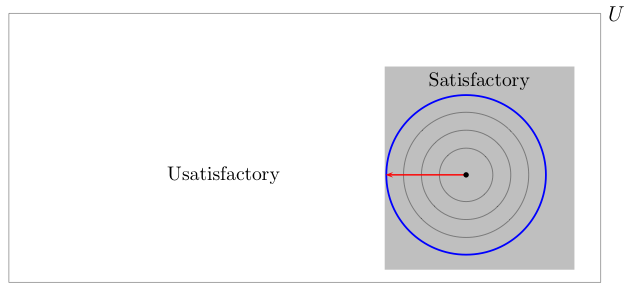 |
Radius of Stability of decision q'' | 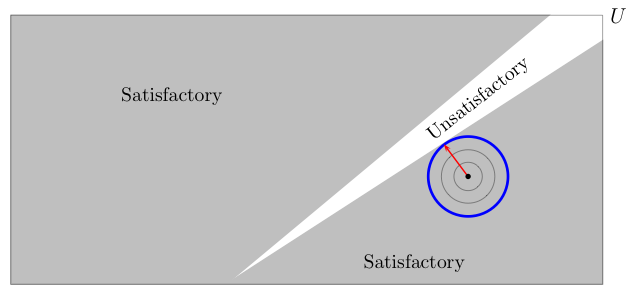 |
Note that while decision q' satisfies the performance constraint only over a very small subset of U, decision q'' satisfies the performance requirement over a very large subset of U. But, according to the precepts of info-gap decision theory, decision q' is more robust than decision q'', even though decision q'' is much more robust than decision q'' insofar as its performance over the entire uncertainty space U is concerned.
The point is then that under severe uncertainty the quality of the estimate û is questionable in the extreme, indeed it can be no more than a wild guess. There are therefore no grounds to assume that the true value of u is more likely to be in the neighborhood of û then in any other neighborhood of U. Which means that the proposition to deploy a local model of robustness to pursue decisions that are robust in the neighborhood of û in total disregard to the rest of the uncertainty space, is the exact antithesis of what a methodology for seeking decisions that are robust to severe uncertainhty ought to be.
To put it more starkly: info-gap decision theory prescription for handling severe uncertainty comes down to this:
- Ignore the severity of the uncertainty under consideration.
- Focus instead on the neighborhood of the given estimate.
- Don't worry about the poor quality of the estimate and the vastness of the uncertainty space.
If this is not a sure recipe for sweeping "major risks under the carpet" what is?
But, this prescription is put forward by info-gap decision theory not only as particularly suitable for problems characterized by unbounded uncertainty spaces! It has recently been proposed (Ben-Haim, 2010) as a reliable tool for handling surprises, rare events, catastrophes, shocks etc. in economic decision and policy making!
And there is even a suggestion that this approach is a suitable tool for handling Black Swans and Unknown Unknowns (see Review 17).
In a nutshell, this proposition is in direct contravention of the following two universally accepted maxims:
- Garbage In -- Gabage Out (GIGO)
- Results can be only as good as the estimates on which they are based.
So, to justify its merits, one must prove (not just waltz around it) that a local analysis in the neighborhood of a wild guess provides a reliable tool for managing severe uncertainty manifested in a vast (indeed unbounded) uncertainty space and a poor estimate.
To put across to readers who do not appreciate the full implications of my argument that a local analysis a la info-gap decision theory (around a poor estimate that can be substaintially wrong in a vast uncertainty space) not only " sweeps major risks under the carpet" but is in fact absurd, consider the following picture:
| No Man's Land | û | No Man's Land |
| -∞ <-------------- | Complete region of uncertainty under consideration | --------------> ∞ |
where
| û | denotes the estimate of the parameter of interest. | |
| denotes the complete region of uncertainty under consideration. | ||
| represents the region of uncertainty that actually affects the results | ||
| generated by info-gap's robustness analysis. | ||
| No Man's Land | represents the vast part of the complete region of uncertainty that has no | |
| impact whatsoever on the results generated by info-gap's robustness model. | ||
Clearly, what this picture makes vivid is that the vaster the uncertainty space, namely the more severe the uncertainty, the greater the absurd in employing info-gap's prescription for severe uncertainty. In other words, it is absurd enough to employ a radius of stability model to model, analyze and manage situations that are subject to severe uncertainty (manifested in unbounded uncertainty spaces). So, to propose that this is a "reliable method" capable of dealing with the surprises, rare events, catastrophes, shocks etc. that complex economic systems are subject to is....!
As I have been arguing all along, this is a prescription for voodoo decision-making.
Comments on Ben-Haim's answer to FAQ 1.
TBA, so stay tuned!FAQ 2: Are Info-Gap Models of Uncertainty Based on the Principle of Ignorance?
Ben-Haim elaborates this question as follows:Question: Are info-gap models of uncertainty based on the principle of ignorance (also known as the principle of insuffient reason, or maximum entropy)? Do info-gap models implicitly assume a uniform probability distribution?
I have no idea who raised this question. It most certainly was not raised by me.
In any event, my answer to it is as follows:
Moshe's Answer:
Info-gap models of uncertainty are not based on Laplace's Principle of Insufficient Reason. Info-gap's robustness model is based on a local worst-case approach to uncertainty. That is, the underlying assumption here is that Nature (namely Uncertainty) always selects the most undesirable (worst) outcome (for the decision maker). So, in the case of info-gap's robustness model, if the decision maker selects decision q and a radius of uncertainty α, Nature (Uncertainty) will select the worst u in the ball U(α,û) insofar as the performance requirement r* ≤ r(q,u) is concerened. For instance, She may select the value of u in the ball U(α,û) that minimizes the value of r(q,u) (see FAQ 1).
In contrast, info-gap's opportuneness model (see discussion elswhere) is based on a local best-case approach. That is, the assumption is that Nature (namely Uncertainty) always selects the most desirable (best) outcome (for the decision maker). So, in the case of info-gap's opportunenss model, if the decision maker selects decision q and a radius of uncertainty α, Nature (Uncertainty) will select the best u in the ball U(α,û) insofar as the performance requirement r* ≤ r(q,u) is concerened. For instance, She may select the value of u in the ball U(α,û) that maximizes the value of r(q,u). The radius of opportuneness of decision q is the radius of the smallest ball centered at û that is tangent to the region of stability associated with q (here the estimate is assumed to be outside the region of stability).
FAQ 3: Is Robust-Satisficing the Same as Max-Min?
Ben-Haim elaborates this question as follows:
Question: Is info-gap theory simply a re-invention of the max-min principle? Does info-gap robust-satisficing lead to the same decisions as a max-min decision strategy?
As a prelude, it is important to point out the staggering presumption underlying the question:
Is info-gap theory simply a re-invention of the max-min principle?
The presumption is staggering because it attempts to put info-gap's robustness model and Wald's Maximin model on an equal footing. Namely, the underlying assumption here is that info-gap's robustness model and Wald's Maximin model are on a par and can therefore be compared as "equals" (more or less).
But, as the answer to this question demonstrates, even the phrasing of this question is misleading, because the question that should have been ask is this:
Question: What exactly is the relation between info-gap's robustness model and Wald's Maximin model? And what exactly is the relation between info-gap's decision model and Wald's Maximin model?
And the answer to this question is very simple:
Answer: Both info-gap's robustness model and info-gap's decision models are simple instances (cases) of Wald's Maximin model.Indeed, Wald's Maximin model is incomparably more general and powerful than info-gap's robustness model and info-gap's decision model.
You may wish to read the formal proof that info-gap's robustness model is a simple instance of Wald's Maximin model.
I should point out that Ben-Haim is fully aware of the existence of such proofs and that he does not dispute their validity.
Now back to Ben-Haim's question.
The answer to this question is crystal clear:
Moshe's Answer:
- Info-gap decision theory is not a re-invention of the maximin principle, simply because one cannot even presume that it can be a re-invention of the maximin principle.
- This is so because info-gap's decision model is a simple instance of Wald's maximin model.
- And, info-gap's robustness model is a simple instance of Wald's maximin model.
- And, info-gap's opportuneness model is a simple instance of the classic Minimin model.
The only meaningful comparison that can possibly be made would be a comparison between specific instances of Wald's Maximin model and info-gap's generic robustness and decision models. Consequently, the only way to answer the question: "Does info-gap robust-satisficing lead to the same decisions as a max-min decision strategy?" is by working out an answer to the following question:
Is there an instance of Wald's Maximin model that yields exactly the same results as those yielded by info-gap's robustness model?And the answer to this is straightforward.
It is elementary to construct a simple Maximin model (see proof) that is fully equivalent to info-gap's robustness model. This means that, as fully equivalent to info-gap's robustness model, this simple Maximin model always generates exactly the same results as those generated by info-gap's robustness model.For your convenience, here are the two models in question:
Info-gap's robustness model Equivalent Maximin model max {α≥0: r* ≤ r(q,u),∀u∈U(α,û)} ≡
max min f(q,α,u) α≥0 u∈U(α,û) where f(q,α,u) := α if r*≤ r(q,u) and f(q,α,u) := −∞ if r*> r(q,u).
To see that these two models are indeed equivalent, hence generate the same results, go to the proof.
For info-gap's decision model we obain the following equivalence:
Info-gap's decision model Equivalent Maximin model
max max {α≥0: r* ≤ r(q,u),∀u∈U(α,û)} ≡ q∈Q
max min f(q,α,u) α≥0 u∈U(α,û) This should make it clear that the question "Is info-gap theory simply a re-invention of the max-min principle?" amounts to a misrepresentation of the relation between info-gap's generic model and Wald's maximin model.
To complete the argument, I should point out of course that the only sense in which one can ask whether or not info-gap's robustness model is a "re-invention" is with regard to its relation to the Radius of Stability model.
And the answer to this is: yes of course! Info-gap's robustness model is a reinvention of the Radius of Stability model (circa 1960).
However, the trouble is that as the info-gap methodology prescribes a misapplication of the Radius of Stability model, info-gap's robustness model ends being a reinvented square wheel.
FAQ 4: Can the Max-Min Strategy be Used to Describe Robust-Satisficing Behavior?
Ben-Haim elaborates this question as follows:Question: Can the max-min strategy always be used to describe robust-satisficing behavior?
The answer to is obvious:
Moshe's Answer:This question is utterly redundant, meaning that there is no ground to so much as contemplate it.
This is so simply because info-gap's robustness model is a simple instance of Wald's Maximin model. In fact, one can easily construct (see the formal proof) a Maximin model that will mimic exactly info-gap's robustness model behavior. Put another way, there is nothing that info-gap's robustness model can do that the instance of Wald's Maximin model in question would be unable to do. This is a direct implication of the answer to FAQ 3. The same is true with reagrd to info-gap's decision model.
FAQ 5: Does Maximum Robustness Imply Maximum Likelihood of Success?
Ben-Haim expands this question as follows:Question: Does maximum robustness imply maximum likelihood of success? Even though an info- gap model of uncertainty is non-probabilistic, does the info-gap robustness function nonetheless reveal something about the underlying probability?
My answer to this question is crystal clear:
Moshe's Answer:No, of course not!
"Info-gap's robustness" and "likelihood of success" are two entirely different concepts that are associated with two entirely different models, giving expression to two fundamentally different situations. As a rule therefore, maximum robustness (according to the precepts of info-gap decision theory) does not/cannot imply maximum likelihood of success.
Needless to say, under certain severe conditions, it is possible to formulate info-gap's robustness model so that it will mimic the behavior of likelihood models. But this is limited only to special, for the most part trivial, cases.
Consider for instance the following quote:
We have shown that the definition of strong proxy theorems discussed by Ben-Haim (2007), is very restrictive, and that when the uncertainty is multi-dimensional, strong proxy theorems are expected to be very rare. Then we shall prove that even this weaker definition does not hold for a wide family of common problems.
Lior Davidovitch (2009, p. 137)
Strategic Interactions Under Severe Uncertainty
PhD Thesis, Department of Mechanical Engineering,
The Technion -- Israel Istitutue of Technology
Haifa, Israel
Suffice it to say that there is a long list of reasons for (reasonably) assuming that when the uncertainty is severe such proxy theorems will be very rare, and should be expected to be valid only in trivial cases.
Hint: For the idea behind this enterprise to make any sense at all, you would have to attribute info-gap's robustness model a likelihood structure such that the likelihood would be local, namely it would have to be concentrated around the estimate û. Your assumption would then be that, the "bulk" of the likelihood must be located in the neighborhood of the estimate. But, how would this assumption tally with the basic assumption that the uncertainty under consideration is severe? Surely, the two assumptions exclude one another!
Indeed, to see how lacking in merit this idea is, assume that the uncertainty space is a box in the n-dimentional Eucledian space and that the likelihood structure is "uniform". For the proxy idea to work here, the local robustness of the decisions in the neighborhood of the estimate would have to reflect (be consistent with) their global robustness over U. But this would be the case only in extremely "naive" cases. For example, in one dimensional uncertainty spaces with strong monotonicity conditions on the performance function.
FAQ 6: Can Max-Min Computational Tools be Used for Info-Gap Robustness?
Ben-Haim elaborates this question as follows:
Question: A lot of effort in statistics goes into finding methods for determining max-min strategies and estimators. Can these tools be used for calculating info-gap robustness functions?
The expanded version is most telling.
The reference to "statistics" begs the question, because closer to home is classical decision theory and robust optimization. The question that ought to have been asked then is about the tools worked out for robust decision-making? After all, info-gap decision theory is claimed to be ... a decision theory for robust decision (in the face of severe uncertainty). Indeed, its robustness and decision models are Maximin type formulations of (robust) optimization problems. So, the methods and algorithms that are immediately relevant to info-gap decision theory are those used in the area of robust optimization, for the solution of Maximin problems. But this fact is not even alluded to!
It should be pointed out therefore that this (inexcusable) total oblivion to the state of the art in robust optimization is endemic in the info-gap literature.
Remark:
Since info-gap's robustness model is a simple radius of stability model, comutational tools developed for generic radius of stability models could be useful here.
FAQ 7: Can Info-Gap Theory Deal with Multiple Performance Requirements?
This question addresses in fact two separate issues. The modeling issue and the algorithmic issue.
From a modeling point of view, radius of stability models, such as info-gap's robustness model, can incorporate any number of performace requirements, in fact as many as one wishes, and these can be as complicated as can be.
However, dealing with multiple performance requirements algorithmically is a different kettle of fish. Multiple performance requirements can greatly complicate the algorithm (solution procedure) to impede the solution of the problem altogether. This is particularly true for problems with single performanace requirement that are easily amenable to an analytic closed-form solution. Such problems may prove utterly intractable when additional performance requirement are incorporated in the formulation of the problem.
The reason that I am calling attention to this (no doubt obvious) fact is that the illustration of info-gap's robustness model, in the Info-gap literature, is generally done through the medium of problems with single performanace requirement. My point is then that this can give the wrong impression about info-gap's true capabilities.
In any event, my answer to this question is this:
There are no general purpose algorithms for robust optimization problems associated info-gap robustness model. For this reason alone it is important for info-gap adherents to become acquainted with the area of robust optimization.
Other Reviews
- Ben-Haim (2001, 2006): Info-Gap Decision Theory: decisions under severe uncertainty.
- Regan et al (2005): Robust decision-making under severe uncertainty for conservation management.
- Moilanen et al (2006): Planning for robust reserve networks using uncertainty analysis.
- Burgman (2008): Shakespeare, Wald and decision making under severe uncertainty.
- Ben-Haim and Demertzis (2008): Confidence in monetary policy.
- Hall and Harvey (2009): Decision making under severe uncertainty for flood risk management: a case study of info-gap robustness analysis.
- Ben-Haim (2009): Info-gap forecasting and the advantage of sub-optimal models.
- Yokomizo et al (2009): Managing the impact of invasive species: the value of knowing the density-impact curve.
- Davidovitch et al (2009): Info-gap theory and robust design of surveillance for invasive species: The case study of Barrow Island.
- Ben-Haim et al (2009): Do we know how to set decision thresholds for diabetes?
- Beresford and Thompson (2009): An info-gap approach to managing portfolios of assets with uncertain returns
- Ben-Haim, Dacso, Carrasco, and Rajan (2009): Heterogeneous uncertainties in cholesterol management
- Rout, Thompson, and McCarthy (2009): Robust decisions for declaring eradication of invasive species
- Ben-Haim (2010): Info-Gap Economics: An Operational Introduction
- Hine and Hall (2010): Information gap analysis of flood model uncertainties and regional frequency analysis
- Ben-Haim (2010): Interpreting Null Results from Measurements with Uncertain Correlations: An Info-Gap Approach
- Wintle et al. (2010): Allocating monitoring effort in the face of unknown unknowns
- Moffitt et al. (2010): Securing the Border from Invasives: Robust Inspections under Severe Uncertainty
- Yemshanov et al. (2010): Robustness of Risk Maps and Survey Networks to Knowledge Gaps About a New Invasive Pest
- Davidovitch and Ben-Haim (2010): Robust satisficing voting: why are uncertain voters biased towards sincerity?
- Schwartz et al. (2010): What Makes a Good Decision? Robust Satisficing as a Normative Standard of Rational Decision Making
- Arkadeb Ghosal et al. (2010): Computing Robustness of FlexRay Schedules to Uncertainties in Design Parameters
- Hemez et al. (2002): Info-gap robustness for the correlation of tests and simulations of a non-linear transient
- Hemez et al. (2003): Applying information-gap reasoning to the predictive accuracy assessment of transient dynamics simulations
- Hemez, F.M. and Ben-Haim, Y. (2004): Info-gap robustness for the correlation of tests and simulations of a non-linear transient
- Ben-Haim, Y. (2007): Frequently asked questions about info-gap decision theory
- Sprenger, J. (2011): The Precautionary Approach and the Role of Scientists in Environmental Decision-Making
- Sprenger, J. (2011): Precaution with the Precautionary Principle: How does it help in making decisions
- Hall et al. (2011): Robust climate policies under uncertainty: A comparison of Info--Gap and RDM methods
- Ben-Haim and Cogan (2011) : Linear bounds on an uncertain non-linear oscillator: an info-gap approach
- Van der Burg and Tyre (2011) : Integrating info-gap decision theory with robust population management: a case study using the Mountain Plover
- Hildebrandt and Knoke (2011) : Investment decisions under uncertainty --- A methodological review on forest science studies.
- Wintle et al. (2011) : Ecological-economic optimization of biodiversity conservation under climate change.
- Ranger et al. (2011) : Adaptation in the UK: a decision-making process.
Recent Articles, Working Papers, Notes
Also, see my complete list of articles
Moshe's new book! - Sniedovich, M. (2012) Fooled by local robustness, Risk Analysis, in press.
- Sniedovich, M. (2012) Black swans, new Nostradamuses, voodoo decision theories and the science of decision-making in the face of severe uncertainty, International Transactions in Operational Research, in press.
- Sniedovich, M. (2011) A classic decision theoretic perspective on worst-case analysis, Applications of Mathematics, 56(5), 499-509.
- Sniedovich, M. (2011) Dynamic programming: introductory concepts, in Wiley Encyclopedia of Operations Research and Management Science (EORMS), Wiley.
- Caserta, M., Voss, S., Sniedovich, M. (2011) Applying the corridor method to a blocks relocation problem, OR Spectrum, 33(4), 815-929, 2011.
- Sniedovich, M. (2011) Dynamic Programming: Foundations and Principles, Second Edition, Taylor & Francis.
- Sniedovich, M. (2010) A bird's view of Info-Gap decision theory, Journal of Risk Finance, 11(3), 268-283.
- Sniedovich M. (2009) Modeling of robustness against severe uncertainty, pp. 33- 42, Proceedings of the 10th International Symposium on Operational Research, SOR'09, Nova Gorica, Slovenia, September 23-25, 2009.
- Sniedovich M. (2009) A Critique of Info-Gap Robustness Model. In: Martorell et al. (eds), Safety, Reliability and Risk Analysis: Theory, Methods and Applications, pp. 2071-2079, Taylor and Francis Group, London.
.
- Sniedovich M. (2009) A Classical Decision Theoretic Perspective on Worst-Case Analysis, Working Paper No. MS-03-09, Department of Mathematics and Statistics, The University of Melbourne.(PDF File)

- Caserta, M., Voss, S., Sniedovich, M. (2008) The corridor method - A general solution concept with application to the blocks relocation problem. In: A. Bruzzone, F. Longo, Y. Merkuriev, G. Mirabelli and M.A. Piera (eds.), 11th International Workshop on Harbour, Maritime and Multimodal Logistics Modeling and Simulation, DIPTEM, Genova, 89-94.
- Sniedovich, M. (2008) FAQS about Info-Gap Decision Theory, Working Paper No. MS-12-08, Department of Mathematics and Statistics, The University of Melbourne, (PDF File)

- Sniedovich, M. (2008) A Call for the Reassessment of the Use and Promotion of Info-Gap Decision Theory in Australia (PDF File)
- Sniedovich, M. (2008) Info-Gap decision theory and the small applied world of environmental decision-making, Working Paper No. MS-11-08
This is a response to comments made by Mark Burgman on my criticism of Info-Gap (PDF file)
- Sniedovich, M. (2008) A call for the reassessment of Info-Gap decision theory, Decision Point, 24, 10.
- Sniedovich, M. (2008) From Shakespeare to Wald: modeling wors-case analysis in the face of severe uncertainty, Decision Point, 22, 8-9.
- Sniedovich, M. (2008) Wald's Maximin model: a treasure in disguise!, Journal of Risk Finance, 9(3), 287-291.
- Sniedovich, M. (2008) Anatomy of a Misguided Maximin formulation of Info-Gap's Robustness Model (PDF File)
In this paper I explain, again, the misconceptions that Info-Gap proponents seem to have regarding the relationship between Info-Gap's robustness model and Wald's Maximin model.
- Sniedovich. M. (2008) The Mighty Maximin! (PDF File)
This paper is dedicated to the modeling aspects of Maximin and robust optimization.
- Sniedovich, M. (2007) The art and science of modeling decision-making under severe uncertainty, Decision Making in Manufacturing and Services, 1-2, 111-136. (PDF File)
.
- Sniedovich, M. (2007) Crystal-Clear Answers to Two FAQs about Info-Gap (PDF File)
In this paper I examine the two fundamental flaws in Info-Gap decision theory, and the flawed attempts to shrug off my criticism of Info-Gap decision theory.
- My reply (PDF File)
to Ben-Haim's response to one of my papers. (April 22, 2007)
This is an exciting development!
- Ben-Haim's response confirms my assessment of Info-Gap. It is clear that Info-Gap is fundamentally flawed and therefore unsuitable for decision-making under severe uncertainty.
- Ben-Haim is not familiar with the fundamental concept point estimate. He does not realize that a function can be a point estimate of another function.
So when you read my papers make sure that you do not misinterpret the notion point estimate. The phrase "A is a point estimate of B" simply means that A is an element of the same topological space that B belongs to. Thus, if B is say a probability density function and A is a point estimate of B, then A is a probability density function belonging to the same (assumed) set (family) of probability density functions.
Ben-Haim mistakenly assumes that a point estimate is a point in a Euclidean space and therefore a point estimate cannot be say a function. This is incredible!
- A formal proof that Info-Gap is Wald's Maximin Principle in disguise. (December 31, 2006)
This is a very short article entitled Eureka! Info-Gap is Worst Case (maximin) in Disguise! (PDF File)
It shows that Info-Gap is not a new theory but rather a simple instance of Wald's famous Maximin Principle dating back to 1945, which in turn goes back to von Neumann's work on Maximin problems in the context of Game Theory (1928).
- A proof that Info-Gap's uncertainty model is fundamentally flawed. (December 31, 2006)
This is a very short article entitled The Fundamental Flaw in Info-Gap's Uncertainty Model (PDF File).
It shows that because Info-Gap deploys a single point estimate under severe uncertainty, there is no reason to believe that the solutions it generates are likely to be robust.
- A math-free explanation of the flaw in Info-Gap. ( December 31, 2006)
This is a very short article entitled The GAP in Info-Gap (PDF File).
It is a math-free version of the paper above. Read it if you are allergic to math.
- A long essay entitled What's Wrong with Info-Gap? An Operations Research Perspective (PDF File)
(December 31, 2006).
This is a paper that I presented at the ASOR Recent Advances in Operations Research (PDF File)mini-conference (December 1, 2006, Melbourne, Australia).
Recent Lectures, Seminars, Presentations
If your organization is promoting Info-Gap, I suggest that you invite me for a seminar at your place. I promise to deliver a lively, informative, entertaining and convincing presentation explaining why it is not a good idea to use — let alone promote — Info-Gap as a decision-making tool.
Here is a list of relevant lectures/seminars on this topic that I gave in the last two years.
ASOR Recent Advances, 2011, Melbourne, Australia, November 16 2011. Presentation: The Power of the (peer-reviewed) Word. (PDF file).
- Alex Rubinov Memorial Lecture The Art, Science, and Joy of (mathematical) Decision-Making, November 7, 2011, The University of Ballarat. (PDF file).
- Black Swans, Modern Nostradamuses, Voodoo Decision Theories, and the Science of Decision-Making in the Face of Severe Uncertainty (PDF File)
.
(Invited tutorial, ALIO/INFORMS Conference, Buenos Aires, Argentina, July 6-9, 2010).
- A Critique of Info-Gap Decision theory: From Voodoo Decision-Making to Voodoo Economics(PDF File)
.
(Recent Advances in OR, RMIT, Melbourne, Australia, November 25, 2009)
- Robust decision-making in the face of severe uncertainty(PDF File)
.
(GRIPS, Tokyo, Japan, October 16, 2009)
- Decision-making in the face of severe uncertainty(PDF File)
.
(KORDS'09 Conference, Vilnius, Lithuania, September 30 -- OCtober 3, 2009)
- Modeling robustness against severe uncertainty (PDF File)
.
(SOR'09 Conference, Nova Gorica, Slovenia, September 23-25, 2009)
- How do you recognize a Voodoo decision theory?(PDF File)
.
(School of Mathematical and Geospatial Sciences, RMIT, June 26, 2009).
- Black Swans, Modern Nostradamuses, Voodoo Decision Theories, Info-Gaps, and the Science of Decision-Making in the Face of Severe Uncertainty (PDF File)
.
(Department of Econometrics and Business Statistics, Monash University, May 8, 2009).
- The Rise and Rise of Voodoo Decision Theory.
ASOR Recent Advances, Deakin University, November 26, 2008. This presentation was based on the pages on my website (voodoo.moshe-online.com).
- Responsible Decision-Making in the face of Severe Uncertainty (PDF File)
.
(Singapore Management University, Singapore, September 29, 2008)
- A Critique of Info-Gap's Robustness Model (PDF File)
.
(ESREL/SRA 2008 Conference, Valencia, Spain, September 22-25, 2008)
- Robust Decision-Making in the Face of Severe Uncertainty (PDF File)
.
(Technion, Haifa, Israel, September 15, 2008)
- The Art and Science of Robust Decision-Making (PDF File)
.
(AIRO 2008 Conference, Ischia, Italy, September 8-11, 2008 )
- The Fundamental Flaws in Info-Gap Decision Theory (PDF File)
.
(CSIRO, Canberra, July 9, 2008 )
- Responsible Decision-Making in the Face of Severe Uncertainty (PDF File)
.
(OR Conference, ADFA, Canberra, July 7-8, 2008 )
- Responsible Decision-Making in the Face of Severe Uncertainty (PDF File)
.
(University of Sydney Seminar, May 16, 2008 )
- Decision-Making Under Severe Uncertainty: An Australian, Operational Research Perspective (PDF File)
.
(ASOR National Conference, Melbourne, December 3-5, 2007 )
- A Critique of Info-Gap (PDF File)
.
(SRA 2007 Conference, Hobart, August 20, 2007)
- What exactly is wrong with Info-Gap? A Decision Theoretic Perspective (PDF File)
.
(MS Colloquium, University of Melbourne, August 1, 2007)
- A Formal Look at Info-Gap Theory (PDF File)
.
(ORSUM Seminar , University of Melbourne, May 21, 2007)
- The Art and Science of Decision-Making Under Severe Uncertainty (PDF File)
.
(ACERA seminar, University of Melbourne, May 4, 2007)
- What exactly is Info-Gap? An OR perspective. (PDF File)
ASOR Recent Advances in Operations Research mini-conference (December 1, 2006, Melbourne, Australia).
Disclaimer: This page, its contents and style, are the responsibility of the author (Moshe Sniedovich) and do not represent the views, policies or opinions of the organizations he is associated/affiliated with.