The Spin Stops Here!
Decision-Making Under Severe Uncertainty  
Faqs | Help | @ | Contact | home  
voodoostan info-gap decision theory info-gap economics severe uncertainty mighty maximin robust decisions responsible decisions

The Mobile Maximin Theorem

Last modified:

Some info-gap scholars do a lot of traveling.

Apparently, on the road they do not have easy access to my Maximin Theorem. Just in case you have not encountered this theorem before, I add parenthetically that this theorem states that info-gap's robustness model is a simple instance of Wald's famous Maximin model.

In any event, this lack of easy access may explain why so many info-gap articles continue to misrepresent the true relation between info-gap's robustness model and Wald's famous Maximin model.

In fact, Prof. Yakov Ben-Haim -- the Father of Info-gap decision theory -- continues to insist that info-gap robustness model is not a Maximin model. For example, in his latest book Info-Gap Economics we read this (Ben-Haim 2010, page 9):

Info-gap theory is related to robust-control and min-max methods, but nevertheless different from them. The strategy advocated here is not the amelioration of purportedly worst cases.

This is a significant improvement on Ben-Haim's (2001, 2006) earlier unfounded claims that his theory is fairly new and radically different from all current theories of decision under uncertainty.

Still, the complete lack of understanding as to what Wald's Maximin is all about, and the role and place it has in decision theory –- that pervades the earlier statements is manifested in this statement as well.

The trouble is, however, that unfounded erroneous statements such as these help to sustain the myths about info-gap decision theory that continue to circulate in the info-gap literature. Indeed, such statements continue to sustain those info-gap scholars who are still unwilling to face the fact that info-gap decision theory amounts to much ado about nothing, in fact a reinvention of a wheel, and a square one at that! (see my FAQs about info-gap decision theory).

Be that as it may, to remedy the situation, namely to enable easy access to it, I created a mobile version of the theorem. If you are unable to read it on the upper right corner of this page, you can show/hide a magnified version of the theorem and its short proof. Feel free to copy it and carry it with you. However, you should read the Travel Advice.

Alternatively, you may want to carry with you the Mobile Radius of Stability Theorem that I created for similar purposes. It is much more compact. On second thought, to play it safe, you may want to carry both.

Travel Advice

Reading the info-gap literature, one gets the impression that the academic authorities in some countries have banned the use of the Maximin Theorem. You are therefore advised to contact the Customs authorities on arrival to clarify this matter. Because, the last thing you need is to go through the trouble of attempting to explain the details of the proof to Customs officials.

If you are stopped for inspection, you can tell the officials that the theorem and proof have been in the public domain since the end of 2006, that they are completely harmless, and have been fumigated regularly since then.

If they ask you to surrender your copy of the theorem, don't argue with them ... just do it!

And one more thing.

Some of the Customs dogs have photographic memory. So they may indicate to you that they have seen other proofs of the theorem, in which case I suggest that you simply thank them for the tip, pet them on the head and back, as usual, and follow their instructions.

They are usually very friendly and well trained. They may even be able to help you with technical queries regarding the Theorem and the proof.

In case of an emergency, don't hesitate to contact me. But if you are too shy to do that, you may prefer to consult my compilation of FAQs about info-gap decision theory.

Math-free Zone

Several misconceptions about Wald's Mighty Maximin model are systematically circulated in the info-gap literature. I suspect that this may be due to difficulties that some info-gap scholars have in coping with the mathematical aspects of the model.

So, to be able to explain in a math-free fashion why info-gap's robustness model is indeed a Maximin model par excellence, albeit a very simple one, it is instructive to present a math-free portrayal of the model.

Let us begin then with this:

Maximin Rule

Rank alternatives on the basis of their worst-case outcome. That is, select the decision whose worst outcome is at least as good as the worst outcome of any other alternative.

Example:

Suppose that there are four alternative, call them A1, A2, A3 and A4. Also assume that the worst outcomes associated with these alternatives are as follows:

Alternative    Worst outcome
A13
A25
A32
A41

where the outcomes are ... number of dark chocolate bars associated with the four alternatives.

So, if you love dark chocolate the best alternative according to the Maximin rule is .... A2.


It is instructive to explain the working of this rule with the aid of a conceptual game involving two players: the decision maker (DM) and Nature, the latter representing Uncertainty.

It is Nature's job to determine the worst outcome pertaining to the alterative selected by the DM. In this sense Nature is a hostile adversary of the DM. To facilitate this arrangement, we let Nature decide on the state of the system. So, more formally, DM selects an alternative α in A and in response Natures selects a state s in S(α), where A denotes the set of alternatives available to the DM, and S(α) denotes the set of states available to Nature after DM selects alternative a.

To guide their choice of a (alternative state) pair, we introduce the .... outcomes. Let O(α,s) denote the outcome of the game given that DM selected alternative α and Nature selected state s. We assume that the outcomes are real numbers, and that the DM seeks to generate the largest outcome possible --- hence Nature seeks to generate the smallest outcome possible.

Minimax Game

Step 1: DM selects an alternative α in A.

Step 2: Natures select a state a in S(α).

Step 3: The outcome O(α,s) is generated.

Note that since Nature is a hostile adversary, if DM selects alternative α, then Nature will select a state s in S(α) that yields the smallest outcome --- compared to the outcomes generated by the other states in S(α).

Back to info-gap's robustness model.

We have to determine the three objects which define a game, namely A, S( α) and O, so that the game will mimic info-gap's robustness model. Recall then that according to info-gap decision theory, the robustness of decision d is the size of the largest neighborhood around the given estimate û of the parameter of interest, such that the decision satisfies the given performance requirement r* ≤ r(d,u) for all the values of u in the neighborhood.

Here is the picture:

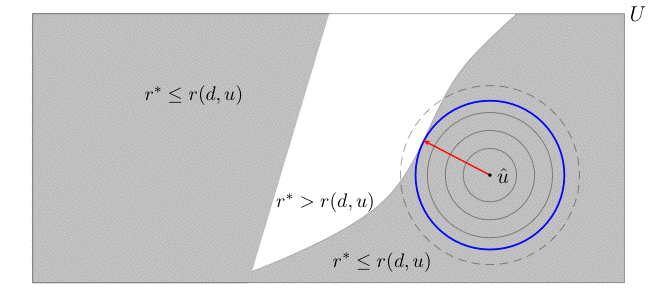
The shaded area represents the set of values of u that satisfy the performance requirement r* ≤ r(d,u). The robustness of decision d is the radius of the largest ball centered at the estimate û that is contained in the shaded area. In the picture it is the radius of the bold blue circle. Note that any increase in the radius of the ball will cause some of the points in the ball to be outside the shaded area.

So, to construct a Maximin model for this problem, we have to determine the objects A, S(a) and O(α,s) of the Maximin game so that the corresponding game will mimic the graphic description given by this picture.

Here is the recipe:

To verify that this setup indeed mimics the picture, consider the following three cases:

  1. Case 1: DM select an α that is smaller than the radius of the blue circle.
    In this case the outcome O(α,s) = a regardless of what state s Nature selects from S(α), as all the states in S(α) satisfy the performance requirement.
    It follows then that DM can select a larger value of α without violating the performance constraint. It is therefore to the DM's advantage to increase the value of α.

  2. Case 2: DM select an α that is larger than the radius of the blue circle.
    In this case there is a state s in S(α) that violates the performance requirement and Nature will definitely select such a state. The outcome will consequently be equal to O(α,s) = −∞ for any such state s.
    Needless to say, it will be to the DM's advantage to decrease the value of α to ensure that no state in S(α) violates the performance requirement.

  3. Case 3: DM select an a that is equal to the radius of the blue circle.
    In this case the DM has no incentive to change the value of α, observing that regardless of what state nature selects from S( α), the outcome O(α,s) is equal to α.
    An increase in the value of a will expand S(α) into the unshaded area, where in response, Nature will select a state that violates the performance constraint. In this case the outcome will be equal to −∞.
    A decrease in the value of α will decrease the value of the outcome O(α,s) = α. Hence, the DM has no incentive to decrease the value of α.

We therefore conclude that the DM will select a value of α that is equal to the radius of the bold blue circle in the picture, namely the radius of the largest ball contained in the shaded area. For her part, Nature can select any point (state) in this circle.

The Mighty Maximin!

I was surprised to learn that quite a few scholars who are involved in the discipline of decision-making have considerable difficulties coping with the modeling aspect of the Maximin paradigm.

So, to "guide the perplexed" I elaborated many of these issues in a long article entitled

The Mighty Maximin

You might be interested in reading this article.

And feel free to use the Maximin bumper sticker

Official Mobile Debunker of info-gap decision theory

Based on the above analysis, it is clear that it is very easy to debunk info-gap decision theory.

In fact, the more Ben-Haim attempts to salvage his theory, the easier it is to demonstrate how wrong he is. In his new book Ben-Haim (2010) claims that his robustness model is different from robustness models used in robust-control and the Maximin/Minimax model. Furthermore, he presents info-gap decision theory as a theory that is a response to the challenge posed by surprises associated with the "economic problem".

DEBUNKED! √
Obviously, Ben-Haim (2001, 2006, 2010) is very wrong on all fronts.

The reader may wish to read my Official Mobile Debunker of info-gap decision theory.

Recent Articles, Working Papers, Notes

Also, see my complete list of articles
    Moshe's new book!
  • Sniedovich, M. (2012) Fooled by local robustness, Risk Analysis, in press.

  • Sniedovich, M. (2012) Black swans, new Nostradamuses, voodoo decision theories and the science of decision-making in the face of severe uncertainty, International Transactions in Operational Research, in press.

  • Sniedovich, M. (2011) A classic decision theoretic perspective on worst-case analysis, Applications of Mathematics, 56(5), 499-509.

  • Sniedovich, M. (2011) Dynamic programming: introductory concepts, in Wiley Encyclopedia of Operations Research and Management Science (EORMS), Wiley.

  • Caserta, M., Voss, S., Sniedovich, M. (2011) Applying the corridor method to a blocks relocation problem, OR Spectrum, 33(4), 815-929, 2011.

  • Sniedovich, M. (2011) Dynamic Programming: Foundations and Principles, Second Edition, Taylor & Francis.

  • Sniedovich, M. (2010) A bird's view of Info-Gap decision theory, Journal of Risk Finance, 11(3), 268-283.

  • Sniedovich M. (2009) Modeling of robustness against severe uncertainty, pp. 33- 42, Proceedings of the 10th International Symposium on Operational Research, SOR'09, Nova Gorica, Slovenia, September 23-25, 2009.

  • Sniedovich M. (2009) A Critique of Info-Gap Robustness Model. In: Martorell et al. (eds), Safety, Reliability and Risk Analysis: Theory, Methods and Applications, pp. 2071-2079, Taylor and Francis Group, London.
    • .
  • Sniedovich M. (2009) A Classical Decision Theoretic Perspective on Worst-Case Analysis, Working Paper No. MS-03-09, Department of Mathematics and Statistics, The University of Melbourne.(PDF File)

  • Caserta, M., Voss, S., Sniedovich, M. (2008) The corridor method - A general solution concept with application to the blocks relocation problem. In: A. Bruzzone, F. Longo, Y. Merkuriev, G. Mirabelli and M.A. Piera (eds.), 11th International Workshop on Harbour, Maritime and Multimodal Logistics Modeling and Simulation, DIPTEM, Genova, 89-94.

  • Sniedovich, M. (2008) FAQS about Info-Gap Decision Theory, Working Paper No. MS-12-08, Department of Mathematics and Statistics, The University of Melbourne, (PDF File)

  • Sniedovich, M. (2008) A Call for the Reassessment of the Use and Promotion of Info-Gap Decision Theory in Australia (PDF File)

  • Sniedovich, M. (2008) Info-Gap decision theory and the small applied world of environmental decision-making, Working Paper No. MS-11-08
    This is a response to comments made by Mark Burgman on my criticism of Info-Gap (PDF file )

  • Sniedovich, M. (2008) A call for the reassessment of Info-Gap decision theory, Decision Point, 24, 10.

  • Sniedovich, M. (2008) From Shakespeare to Wald: modeling wors-case analysis in the face of severe uncertainty, Decision Point, 22, 8-9.

  • Sniedovich, M. (2008) Wald's Maximin model: a treasure in disguise!, Journal of Risk Finance, 9(3), 287-291.

  • Sniedovich, M. (2008) Anatomy of a Misguided Maximin formulation of Info-Gap's Robustness Model (PDF File)
    In this paper I explain, again, the misconceptions that Info-Gap proponents seem to have regarding the relationship between Info-Gap's robustness model and Wald's Maximin model.

  • Sniedovich. M. (2008) The Mighty Maximin! (PDF File)
    This paper is dedicated to the modeling aspects of Maximin and robust optimization.

  • Sniedovich, M. (2007) The art and science of modeling decision-making under severe uncertainty, Decision Making in Manufacturing and Services, 1-2, 111-136. (PDF File) .

  • Sniedovich, M. (2007) Crystal-Clear Answers to Two FAQs about Info-Gap (PDF File)
    In this paper I examine the two fundamental flaws in Info-Gap decision theory, and the flawed attempts to shrug off my criticism of Info-Gap decision theory.

  • My reply (PDF File) to Ben-Haim's response to one of my papers. (April 22, 2007)

    This is an exciting development!

    • Ben-Haim's response confirms my assessment of Info-Gap. It is clear that Info-Gap is fundamentally flawed and therefore unsuitable for decision-making under severe uncertainty.

    • Ben-Haim is not familiar with the fundamental concept point estimate. He does not realize that a function can be a point estimate of another function.

      So when you read my papers make sure that you do not misinterpret the notion point estimate. The phrase "A is a point estimate of B" simply means that A is an element of the same topological space that B belongs to. Thus, if B is say a probability density function and A is a point estimate of B, then A is a probability density function belonging to the same (assumed) set (family) of probability density functions.

      Ben-Haim mistakenly assumes that a point estimate is a point in a Euclidean space and therefore a point estimate cannot be say a function. This is incredible!


  • A formal proof that Info-Gap is Wald's Maximin Principle in disguise. (December 31, 2006)
    This is a very short article entitled Eureka! Info-Gap is Worst Case (maximin) in Disguise! (PDF File)
    It shows that Info-Gap is not a new theory but rather a simple instance of Wald's famous Maximin Principle dating back to 1945, which in turn goes back to von Neumann's work on Maximin problems in the context of Game Theory (1928).

  • A proof that Info-Gap's uncertainty model is fundamentally flawed. (December 31, 2006)
    This is a very short article entitled The Fundamental Flaw in Info-Gap's Uncertainty Model (PDF File) .
    It shows that because Info-Gap deploys a single point estimate under severe uncertainty, there is no reason to believe that the solutions it generates are likely to be robust.

  • A math-free explanation of the flaw in Info-Gap. ( December 31, 2006)
    This is a very short article entitled The GAP in Info-Gap (PDF File) .
    It is a math-free version of the paper above. Read it if you are allergic to math.

  • A long essay entitled What's Wrong with Info-Gap? An Operations Research Perspective (PDF File) (December 31, 2006).
    This is a paper that I presented at the ASOR Recent Advances in Operations Research (PDF File) mini-conference (December 1, 2006, Melbourne, Australia).

Recent Lectures, Seminars, Presentations

If your organization is promoting Info-Gap, I suggest that you invite me for a seminar at your place. I promise to deliver a lively, informative, entertaining and convincing presentation explaining why it is not a good idea to use — let alone promote — Info-Gap as a decision-making tool.

Here is a list of relevant lectures/seminars on this topic that I gave in the last two years.

Disclaimer: This page, its contents and style, are the responsibility of the author (Moshe Sniedovich) and do not represent the views, policies or opinions of the organizations he is associated/affiliated with.


Last modified: