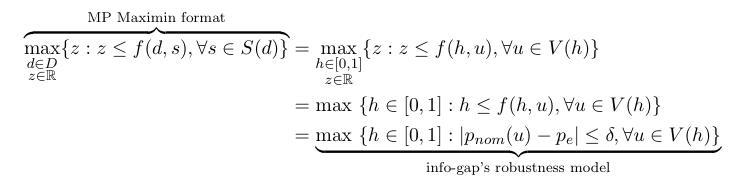The Spin Stops Here!
Decision-Making Under Severe Uncertainty  
Faqs | Help | @ | Contact | home  
voodoostan info-gap decision theory info-gap economics severe uncertainty mighty maximin robust decisions responsible decisions

Reviews of publications on Info-Gap decision theory

Review # 16 (Posted: Ausugst 28, 2010; last update: September 9, 2010)

Reference: Yakov Ben-Haim
Interpreting Null Results from Measurements with Uncertain Correlations: An Info-Gap Approach
Risk Analysis (2010), DOI: 10.1111/j.1539-6924.2010.01485.x
Abstract Null events—not detecting a pernicious agent—are the basis for declaring the agent is absent. Repeated nulls strengthen confidence in the declaration. However, correlations between observations are difficult to assess in many situations and introduce uncertainty in interpreting repeated nulls. We quantify uncertain correlations using an info-gap model, which is an unbounded family of nested sets of possible probabilities. An info-gap model is nonprobabilistic and entails no assumption about a worst case. We then evaluate the robustness, to uncertain correlations, of estimates of the probability of a null event. This is then the basis for evaluating a nonprobabilistic robustness-based confidence interval for the probability of a null.
Keywords Info-gaps; null results; uncertain correlations
Acknowledgments The author is indebted to Mark A. Burgman, Ayala Cohen, David Fox, Malka Gorfine, Mick McCarthy, L. Joe Moffitt, Andrew Robinson, John K. Stranlund, Miriam Zacksenhouse, and an anonymous reviewer for valuable comments. Funding for this research was provided by the U.S. Department of Agriculture under USDA/ERS/PREISM Cooperative Agreement No.58-7000-8-0095.
Scores TUIGF:70%
SNHNSNDN:100%
GIGO:50%

Overview

This is an interesting paper. It is interesting in the sense that it is a perfect illustration of "the more things change the more they stay the same"!

To explain, it is the first paper by the author from which the customary info-gap rhetoric is conspicuously absent. Namely, there is no talk about severe (Knightian) uncertainty, nor about the problem considered being subject to severe uncertainty, nor about the fact that info-gap decision theory offers a particularly suitable method to tackle this task. And most importantly, there is some discussion on Wald's work!

So, at first glance it may appear that the author is finally beginning to take note of the criticism directed at info-gap decision theory to attempt implementing the necessary corrections. But, on closer scrutiny, it turns out that the changes are merely superficial hence misleading. That is, the same obfuscations, the same inaccuracies, hence, the same misleading portrayals of info-gap decision theory and what it does, that populate the author's other publications on info-Gap decision theory, are present in this article as well.

To begin with, there is nothing in this article to give the reader even a clue about:

Hence,

In other words, reading this article one would not have the slightest inkling that Info-gap's robustness model is in fact a simple instance of Wald's Maximin model. Indeed, that it is not just a simple instance of Wald's Maximin model, but a simple radius of stability model. The only reference in the paper that may be construed as vaguely hinting at a possible connection between info-gap's generic model and Wald's Maximin model, is the following enigmatic statement on page 2:

This article uses info-gap theory, which builds on this tradition of nonprobabilistic robustness concepts.

But the point about this statement is that although on the face of it it is somewhat different from the author's customary misleading statements about the purported dissimilarity between info-gap's robustness model and Wald's Maximin model, the statement remains grossly misleading because it conceals more than it reveals. By concealing the fact that info-gap's robustness model is a simple instance of Wald's Maximin model, it gives the false impression that info-gap's robustness model does something that other methods do not do. Or, in the very least, that it adds something to the state of the art.

So, the question is: Does the Info-gap approach proposed in this article offer something that can be construed as a contribution to the state of the art? More generally, does the proposed info-gap approach have any point or merit to recommend it as a sensible/worthwhile/viable approach for the problem considered?

And the answer to this is very simple indeed. Not only that the proposed info-gap model adds nothing to the state of the art, it is in fact completely uncalled for. Because, a quick scan of the problem under consideration and the approach outlined for its treatment reveals the following facts:

In greater detail.

The prolblem is trivial

The problem under consideration in the article is trivial in the same sense that the problem discussed in Review 13 is trivial. Since I discuss this matter in detail in Review 13, I shall not repeat the analysis here.

In brief.

It is rather surprising that the article's reviewers did not see fit to request an explanation/justification for the rational behind the proposed robustness model. The reason that one would have expected the author to explain the point in resorting to a complex approach is obvious. The critical values of the parameter u can be determined simply by inspection. In other words, they can be deduced directly from the performance constraint!

That this is indeed so, is immediately clear. Because, if you strip the problem of its nonessential elements and you focus on its main thrust, you discover that the task it sets is this:

Essence of the Problem:
Determine the largest perturbation u∈[−pnnom , pnom − pnnom] in a given nominal value pnnom ∈[0,1] that does not violate the performance constraint

|pnom(u) − pe| ≤ δ

where
pnom(u) = (1 − α − u)1/n

n is a given positive integer, pe and α are given values in (0,1), and 0 ≤ δ≤ pe.

Clearly, this is a typical radius of stability problem because the idea here is to determine the radius (size) of the largest ball centered at the nominal point, all of whose points satisfy the performance constraint.

But the really interesting point about all this is that --- as u is a numeric scalar --- rather than a vector or a function, the problem is so simple that its solution does not even require the use of a formal radius of stability model. The range of values of u that satisfy the performance constraint can be obtained directly from the constraint itself.

Thus, expressing the performance constraint |pnom(u) − pe| ≤ δ exlicitly in terms of u rather than pnom(u), we obtain

|(1 − α − u)1/n − pe| ≤ δ

which in turn yields

− δ ≤ (1 − α − u)1/n − pe ≤ δ

pe − δ ≤ (1 − α − u)1/n ≤ pe + δ

(pe − δ)n ≤ (1 − α − u) ≤ (pe + δ)n

1 − α − ( pe + δ)n ≤ u ≤ 1 − α − ( pe − δ)n

uL ≤ u ≤ uU

where

uL := 1 − α − ( pe + δ)n

uU := 1 − α − ( pe − δ)n

In short, the range of values of u satisfying the performance constraint is [uL , uU]. One can use any suitable metric or a norm to measure the "size" of this interval. The yielded "size" would then designate the system's robustness.

End of story.

All that info-gap's "uncertainty" model does is to scale and normalize the values of u ... to thereby obscure the simplicity of the problem. Of course, the scaling and normalization can be done, if necessary, after determining the two critical values of u, namely the two end points of the interval of admissible values of u specified above. See discussion in Review 13.

Proposed info-gap uncertainty and robustness models

The author defines the following balls (neighborhoods) around the nominal point pnnom:

U(h) = {pnnom + u : − hpnnom ≤ u ≤ h(pnom − pnnom) } , 0 ≤ h ≤ 1

Thus, U(0) = {pnnom} and U(1) = [0, pnom ].

The associated info-gap robustness model is as follows:

h(pe,δ) = max {h∈[0,1]: |pnom(u) − pe| ≤ δ , ∀u∈V(h)}

where V(h) is the set of admissible values of u induced by U(h), namely V(h) = [-hpnnom,h(pnom − pnnom)] so that V(0)={0} and V(1)=[−pnnom , pnom − pnnom].

Observe that the optimal (maximal) value of h can be obtained directly from the bounds on u specified above.

Radius of stability model

Consider the following generic radius of stability model:

ρ(q,snom):= max {ρ≥0: s∈S(q),∀s∈B(ρ,snom)}

where S(q) denotes the set of the stable states of system q and B(ρ,snom) denotes a ball of radius ρ centered at the nominal state snom. We refer to S(q) as the region of stability of system q.

In words, the radius of stability of system q is the radius of the largest ball contained in the system's region of stability.

By inspection, the robustness model proposed by the author is a radius of stability model characterized by

B(ρ,snom) = V(ρ) , ( h ≡ ρ ; snom = 0)

S(pe) = {u∈[−pnnom , pnom − pnnom ]: |pnom(u) − pe| ≤ δ} , (q ≡ pe ; u ≡ s)

This should come as no surprise given the formal proof that info-gap's generic robustness model is a radius of stability model. This means of course that, any info-gap robustness model is a radius of stability model.

It is important to note that, for over 50 years now, radius of stability models (circa 1960) have beem used extensively in many disciplines ranging from numerical analysis, control theory, economics, optimization, to operations research, and beyond. It is odd therefore that the author does not give the slightest indication that the proposed robustness model is in fact a simple radius of stability model.

Wald's Maximin model

Far more objectionable, however, is the author's ambiguous stance with regard to Wald's Maximin model. Because the author conveniently glosses over the fact that the proposed robustness model is a simple instance of Wald's Maximin model, it is important to remind the reader of the following.

Recall that Wald's Maximin model has two equivalent formats, the classic format and the mathematical programming (MP) format. For our purposes it is concenient to state them as follows:

To show that the proposed info-gap robustness model is a Maximin model, consider the Maximin model specified by the following objects, observing that the correspondence d ≡ h and s ≡ u:

In this case the MP format of the Maximin model is as follows:

So clearly, the proposed info-gap robustness model is a simple Maximin model. This should come as no surprise given the formal proof, dating back to 2007, that info-gap's generic robustness model is a simple instance of Wald's Maximin model. This means of course that, any info-gap robustness model is a Maximin model.

Remarks

1. It is important therefore to take up again the author's oblique reference to the origins of info-gap's robustness model and its place and role in robust decision-making.

Ben-Haim's (2010, p. 2) position      Moshe's clarification thereof
This article uses info-gap theory, which builds on this tradition of non-probabilistic robustness concepts. This portrayal of info-gap's robustness model is grossly misleading because:
  • What may appear to the unsuspecting reader as a statement of historical fact, in effect distorts the whole truth about info-gap's robustness model. It is not a case of this model building on the tradition of nonprobabilistic robustness concepts in the sense of being indebted to this tradition.

  • It is a case of info-gap's robustness model itself being a simple radius of stability model (circa 1960) and as such a very simple instance of Wald's famous Maximin model. So contending that info-gap's robustness model "... builds on ..." Wald's work, is akin to saying that a simple instance of Wald's Maximin model builds on the tradition of Wald's Maximin model.
It is time that the author address these facts fairly and squarely. In fact, this is long overdue.

Of course, it is possible that when the author developed info-gap decision theory in the late 1990s, he was unaware that info-gap's robustness model is just a simple instance of Wald's Maximin model. His erroneous statements from that time should be assessed with this mind.

But the situation has changed dramatically since then.

It has been public knowledge for some time now, that info-gap's robustness model is a simple radius of stability model and a simple instance of Wald's Maximin model. Therefore, statements by the author -- especially in a peer-reviewed article in 2010 -- on the connection between info-gap's robustness model and Wald's Maximin model must be assessed far more critically.

Thus, readers should be interested in my assessment of the author's new book: Info-Gap Economics.

2. The author's narrative on the Wald's(10) (1945) paper is typical Info-gap spin. Having cobbled together half a dozen quotes from this paper he ends up with a paragraph that again conceals more than it reveals. For, consider this: (Ben-Haim 2010, p. 2):

Wald(10) studied the problem of statistical hypothesis testing based on a random sample whose probability distribution is not known, but whose distribution is known to belong to a given class of distribution functions. Wald states that “in most of the applications not even the existence of . . . an a priori probability distribution [on the class of distribution functions] . . . can be postulated, and in those few cases where the existence of an a priori probability distribution . . . may be assumed this distribution is usually unknown.” (p. 267). Wald introduced a loss function expressing the “relative importance of the error committed by accepting” one hypothesized subset of distributions when a specific (though unknown) distribution in fact is true (p. 266). He notes that “the determination of the [loss function] is not a statistical question and is considered here as given” (p. 266). Wald developed a decision procedure that “minimizes the maximum . . . of the risk function” (p. 267).

It is as though the author never heard the term Maximin model. Worse, as though he never heard about the Maximin model's central role in robust decision-making nor about the formal proofs demonstrating that info-gap's robustness model is in fact a Maximin model.

In other words, what the author neglected to add to this uncharacteristically detailed reference to pp. 266-267 in Wald's(10) 1945 paper is something along these lines:

With the founding of modern decision theory in the 1950s, Wald's model was adopted as the foremost paradigm for decision making under severe uncertainty. It is known universally as Maximin model or Minimax model. Today this paradigm plays a central role in robust decision-making, particularly in robust optimization. As for info-gap decision theory's connection to all this, observe that it has been proved formally that info-gap's robustness model is a simple radius of stability model, hence by necessity, a simple instance of Wald's Maximin model.

To get a proper perspective on the author's cryptic, indirect, thus misleading reference to this important paradigm, consider the following:

The entry Robust Control by Noah Williams, Dictionary of Economics, 2008: Huber's (1981, pp. 16-17) book Robust Statistics
Robust control is an approach for confronting model uncertainty in decision making, aiming at finding decision rules which perform well across a range of alternative models. This typically leads to a minimax approach, where the robust decision rule minimizes the worst-case outcome from the possible set. This article discusses the rationale for robust decisions, the background literature in control theory, and different approaches which have been used in economics, including the most prominent approach due to Hansen and Sargent. But as we defined robustness to mean insensitivity with regard to small deviations from assumptions, any quantitative measure of robustness must somehow be concerned with the maximum degradation of performance possible for an ε-deviation from the assumptions. The optimally robust procedure minimizes this degradation and hence will be a minimax procedure of some kind.

If you wonder why the author is so reluctant to accept the basic facts about the "Maximin Connection", note that info-gap decision theory was launched by the author (Ben-Haim 2001, 2006) with great fanfare as unique, novel, and radically different from all other theories for decision under uncertainty. In Ben-Haim's own words (emphasis is mine):

Info-gap decision theory is radically different from all current theories of decision under uncertainty. The difference originates in the modeling of uncertainty as an information gap rather than as a probability. The need for info-gap modeling and management of uncertainty arises in dealing with severe lack of information and highly unstructured uncertainty.
Ben-Haim (2006, p. xii)
In this book we concentrate on the fairly new concept of information-gap uncertainty, whose differences from more classical approaches to uncertainty are real and deep. Despite the power of classical decision theories, in many areas such as engineering, economics, management, medicine and public policy, a need has arisen for a different format for decisions based on severely uncertain evidence.
Ben-Haim (2006, p. 11)

One imagines, therefore, that pulling back from such a position is no easy matter.

I ought to point out that the author continues to uphold this position even if this may not be obvious from the phrasing. Thus, in his new book, Ben-Haim (2010, p. 9) claims that " ... Info-gap theory is related to robust-control and min-max methods, nonetheless different from them. ..." (see my review of this book.)

What exactly is the difference is not made clear in the book!

Other Reviews

  1. Ben-Haim (2001, 2006): Info-Gap Decision Theory: decisions under severe uncertainty.

  2. Regan et al (2005): Robust decision-making under severe uncertainty for conservation management.

  3. Moilanen et al (2006): Planning for robust reserve networks using uncertainty analysis.

  4. Burgman (2008): Shakespeare, Wald and decision making under severe uncertainty.

  5. Ben-Haim and Demertzis (2008): Confidence in monetary policy.

  6. Hall and Harvey (2009): Decision making under severe uncertainty for flood risk management: a case study of info-gap robustness analysis.

  7. Ben-Haim (2009): Info-gap forecasting and the advantage of sub-optimal models.

  8. Yokomizo et al (2009): Managing the impact of invasive species: the value of knowing the density-impact curve.

  9. Davidovitch et al (2009): Info-gap theory and robust design of surveillance for invasive species: The case study of Barrow Island.

  10. Ben-Haim et al (2009): Do we know how to set decision thresholds for diabetes?

  11. Beresford and Thompson (2009): An info-gap approach to managing portfolios of assets with uncertain returns

  12. Ben-Haim, Dacso, Carrasco, and Rajan (2009): Heterogeneous uncertainties in cholesterol management

  13. Rout, Thompson, and McCarthy (2009): Robust decisions for declaring eradication of invasive species

  14. Ben-Haim (2010): Info-Gap Economics: An Operational Introduction

  15. Hine and Hall (2010): Information gap analysis of flood model uncertainties and regional frequency analysis

  16. Ben-Haim (2010): Interpreting Null Results from Measurements with Uncertain Correlations: An Info-Gap Approach

  17. Wintle et al. (2010): Allocating monitoring effort in the face of unknown unknowns

  18. Moffitt et al. (2010): Securing the Border from Invasives: Robust Inspections under Severe Uncertainty

  19. Yemshanov et al. (2010): Robustness of Risk Maps and Survey Networks to Knowledge Gaps About a New Invasive Pest

  20. Davidovitch and Ben-Haim (2010): Robust satisficing voting: why are uncertain voters biased towards sincerity?

  21. Schwartz et al. (2010): What Makes a Good Decision? Robust Satisficing as a Normative Standard of Rational Decision Making

  22. Arkadeb Ghosal et al. (2010): Computing Robustness of FlexRay Schedules to Uncertainties in Design Parameters

  23. Hemez et al. (2002): Info-gap robustness for the correlation of tests and simulations of a non-linear transient

  24. Hemez et al. (2003): Applying information-gap reasoning to the predictive accuracy assessment of transient dynamics simulations

  25. Hemez, F.M. and Ben-Haim, Y. (2004): Info-gap robustness for the correlation of tests and simulations of a non-linear transient

  26. Ben-Haim, Y. (2007): Frequently asked questions about info-gap decision theory

  27. Sprenger, J. (2011): The Precautionary Approach and the Role of Scientists in Environmental Decision-Making

  28. Sprenger, J. (2011): Precaution with the Precautionary Principle: How does it help in making decisions

  29. Hall et al. (2011): Robust climate policies under uncertainty: A comparison of Info-­-Gap and RDM methods

  30. Ben-Haim and Cogan (2011) : Linear bounds on an uncertain non-linear oscillator: an info-gap approach

  31. Van der Burg and Tyre (2011) : Integrating info-gap decision theory with robust population management: a case study using the Mountain Plover

  32. Hildebrandt and Knoke (2011) : Investment decisions under uncertainty --- A methodological review on forest science studies.

  33. Wintle et al. (2011) : Ecological-economic optimization of biodiversity conservation under climate change.

  34. Ranger et al. (2011) : Adaptation in the UK: a decision-making process.

Recent Articles, Working Papers, Notes

Also, see my complete list of articles
    Moshe's new book!
  • Sniedovich, M. (2012) Fooled by local robustness, Risk Analysis, in press.

  • Sniedovich, M. (2012) Black swans, new Nostradamuses, voodoo decision theories and the science of decision-making in the face of severe uncertainty, International Transactions in Operational Research, in press.

  • Sniedovich, M. (2011) A classic decision theoretic perspective on worst-case analysis, Applications of Mathematics, 56(5), 499-509.

  • Sniedovich, M. (2011) Dynamic programming: introductory concepts, in Wiley Encyclopedia of Operations Research and Management Science (EORMS), Wiley.

  • Caserta, M., Voss, S., Sniedovich, M. (2011) Applying the corridor method to a blocks relocation problem, OR Spectrum, 33(4), 815-929, 2011.

  • Sniedovich, M. (2011) Dynamic Programming: Foundations and Principles, Second Edition, Taylor & Francis.

  • Sniedovich, M. (2010) A bird's view of Info-Gap decision theory, Journal of Risk Finance, 11(3), 268-283.

  • Sniedovich M. (2009) Modeling of robustness against severe uncertainty, pp. 33- 42, Proceedings of the 10th International Symposium on Operational Research, SOR'09, Nova Gorica, Slovenia, September 23-25, 2009.

  • Sniedovich M. (2009) A Critique of Info-Gap Robustness Model. In: Martorell et al. (eds), Safety, Reliability and Risk Analysis: Theory, Methods and Applications, pp. 2071-2079, Taylor and Francis Group, London.
    • .
  • Sniedovich M. (2009) A Classical Decision Theoretic Perspective on Worst-Case Analysis, Working Paper No. MS-03-09, Department of Mathematics and Statistics, The University of Melbourne.(PDF File)

  • Caserta, M., Voss, S., Sniedovich, M. (2008) The corridor method - A general solution concept with application to the blocks relocation problem. In: A. Bruzzone, F. Longo, Y. Merkuriev, G. Mirabelli and M.A. Piera (eds.), 11th International Workshop on Harbour, Maritime and Multimodal Logistics Modeling and Simulation, DIPTEM, Genova, 89-94.

  • Sniedovich, M. (2008) FAQS about Info-Gap Decision Theory, Working Paper No. MS-12-08, Department of Mathematics and Statistics, The University of Melbourne, (PDF File)

  • Sniedovich, M. (2008) A Call for the Reassessment of the Use and Promotion of Info-Gap Decision Theory in Australia (PDF File)

  • Sniedovich, M. (2008) Info-Gap decision theory and the small applied world of environmental decision-making, Working Paper No. MS-11-08
    This is a response to comments made by Mark Burgman on my criticism of Info-Gap (PDF file )

  • Sniedovich, M. (2008) A call for the reassessment of Info-Gap decision theory, Decision Point, 24, 10.

  • Sniedovich, M. (2008) From Shakespeare to Wald: modeling wors-case analysis in the face of severe uncertainty, Decision Point, 22, 8-9.

  • Sniedovich, M. (2008) Wald's Maximin model: a treasure in disguise!, Journal of Risk Finance, 9(3), 287-291.

  • Sniedovich, M. (2008) Anatomy of a Misguided Maximin formulation of Info-Gap's Robustness Model (PDF File)
    In this paper I explain, again, the misconceptions that Info-Gap proponents seem to have regarding the relationship between Info-Gap's robustness model and Wald's Maximin model.

  • Sniedovich. M. (2008) The Mighty Maximin! (PDF File)
    This paper is dedicated to the modeling aspects of Maximin and robust optimization.

  • Sniedovich, M. (2007) The art and science of modeling decision-making under severe uncertainty, Decision Making in Manufacturing and Services, 1-2, 111-136. (PDF File) .

  • Sniedovich, M. (2007) Crystal-Clear Answers to Two FAQs about Info-Gap (PDF File)
    In this paper I examine the two fundamental flaws in Info-Gap decision theory, and the flawed attempts to shrug off my criticism of Info-Gap decision theory.

  • My reply (PDF File) to Ben-Haim's response to one of my papers. (April 22, 2007)

    This is an exciting development!

    • Ben-Haim's response confirms my assessment of Info-Gap. It is clear that Info-Gap is fundamentally flawed and therefore unsuitable for decision-making under severe uncertainty.

    • Ben-Haim is not familiar with the fundamental concept point estimate. He does not realize that a function can be a point estimate of another function.

      So when you read my papers make sure that you do not misinterpret the notion point estimate. The phrase "A is a point estimate of B" simply means that A is an element of the same topological space that B belongs to. Thus, if B is say a probability density function and A is a point estimate of B, then A is a probability density function belonging to the same (assumed) set (family) of probability density functions.

      Ben-Haim mistakenly assumes that a point estimate is a point in a Euclidean space and therefore a point estimate cannot be say a function. This is incredible!


  • A formal proof that Info-Gap is Wald's Maximin Principle in disguise. (December 31, 2006)
    This is a very short article entitled Eureka! Info-Gap is Worst Case (maximin) in Disguise! (PDF File)
    It shows that Info-Gap is not a new theory but rather a simple instance of Wald's famous Maximin Principle dating back to 1945, which in turn goes back to von Neumann's work on Maximin problems in the context of Game Theory (1928).

  • A proof that Info-Gap's uncertainty model is fundamentally flawed. (December 31, 2006)
    This is a very short article entitled The Fundamental Flaw in Info-Gap's Uncertainty Model (PDF File) .
    It shows that because Info-Gap deploys a single point estimate under severe uncertainty, there is no reason to believe that the solutions it generates are likely to be robust.

  • A math-free explanation of the flaw in Info-Gap. ( December 31, 2006)
    This is a very short article entitled The GAP in Info-Gap (PDF File) .
    It is a math-free version of the paper above. Read it if you are allergic to math.

  • A long essay entitled What's Wrong with Info-Gap? An Operations Research Perspective (PDF File) (December 31, 2006).
    This is a paper that I presented at the ASOR Recent Advances in Operations Research (PDF File) mini-conference (December 1, 2006, Melbourne, Australia).

Recent Lectures, Seminars, Presentations

If your organization is promoting Info-Gap, I suggest that you invite me for a seminar at your place. I promise to deliver a lively, informative, entertaining and convincing presentation explaining why it is not a good idea to use — let alone promote — Info-Gap as a decision-making tool.

Here is a list of relevant lectures/seminars on this topic that I gave in the last two years.

Disclaimer: This page, its contents and style, are the responsibility of the author (Moshe Sniedovich) and do not represent the views, policies or opinions of the organizations he is associated/affiliated with.


Last modified: