| Reference: |
An info-gap approach to managing portfolios of assets with uncertain returns Bryan Beresford-Smith and Colin J. Thompson Journal of Risk Finance 10(3), 277-287, 2009. |
| Abstract |
Purpose The purpose of this paper is to provide a quantitative methodology based on information-gap decision theory for dealing with (true) Knightian uncertainty in the management of portfolios of assets with uncertain returns.
Design/methodology/approach
Findings
Research limitations/implications
Practical implications Originality/value This paper provides a new and novel approach for managing portfolios in the face of uncertainties in future asset returns. Keywords: Portfolio investment, Financial modelling, Uncertainty management, Information management Paper type: Research paper. |
| Acknowledgement | The authors are grateful to Yakov Ben-Haim for many illuminating discussions on info-gap theory and for a critical reading of an early version of this paper. |
| Scores | TUIGF:100% SNHNSNDN:75% GIGO:100% |
The main reason for my taking up this paper for review is to address a statement made by the authors about results reported on in my 2008 article, which was published in the same journal.
On page 278 of the Beresford-Smith Thompson's (2009) article we read (emphasis is mine):
The main problem with CAPM and related models is that they are based on expected future returns on assets that in principle are unknown and subject to considerable uncertainty. In such situations we are dealing with "true uncertainty" in the sense of Knight (1921) who was the first to distinguish between "risk" based on known probability distributions and true uncertainty when the underlying statistical distributions are unknown. Knight's ideas have been further developed by several authors over the years and in particular by Ben-Haim (2006) who has developed a quantitative formulation known as information-gap decision theory. This theory has recently been shown by Sniedovich (2008) to be formally equivalent to Wald's maximin model in classical decision theory (French, 1988).
This text addresses three prevailing myths about Info-Gap decision theory, namely:
- Myth 1: Info-Gap decision theory is distinct, novel, revolutionary, and radically different from all theories for decision under uncertainty.
- Myth 2: Info-Gap's robustness model is not a Maximin model.
- Myth 3: Info-Gap decision theory is a theory for decision-making under severe uncertainty, eg. true Knightian uncertainty.
In the quoted text the authors dispel Myth 1 and Myth 2 and continue to propagate Myth 3.
Some comments:
- To begin with, it cannot be emphasized enough that Info-Gap decision theory is, as a matter of principle, unable to deal with Knightian uncertainty. Indeed, adopting as it does a local approach to the treatment of uncertainty, hence to robustness against severe uncertainty, Info-Gap's robustness model constitutes the exact antithesis of what a proper/correct/sound treatment of Knightian uncertainty calls for.
For, how can a theory even be expected to meet the challenges posed by severe uncertainty, especially "true" Knightian uncertainty, if it a priori fixes only on a wild guess and limits its entire robustness analysis to the immediate neighborhood of this wild guess?
The answer is: it can't!
The picture is this:
No Man's Land û No Man's Land 
<-------------- Complete region of uncertainty under consideration --------------> where û denotes the estimate of the parameter of interest, the black area represents the complete region of uncertainty under consideration, the red area around û represents the region of uncertainty that actually affects the results generated by Info-Gap's robustness analysis, and the vast No Man's Land represents that part of the complete region of uncertainty that has no impact whatsoever on the results generated by Info-Gap's robustness model.
Clearly, how can one possibly expect Info-Gap decision theory — that as attested by this statement is designed to take on the severest uncertainty imaginable "True Knightian Uncertainty — to deal with Black Swans namely, extreme events that would fall under "True Knightian Uncertainty", if it cannot even handle plain, ordinary, "white swans" that occur in the vast No Man's Land.
And what is the wonder that such a theory cannot possibly be expected to deal with this type of uncertainty?!
After all, Info-Gap's uncertainty and robustness models were originally (Ben-Haim, 1996 ) put forward to deal with a relatively mild uncertainty and variability around given "nominal values". Yet, without the slightest modification having been made in these models to meet the challenges of severe uncertainty, precisely the same models, prescribing precisely the same treatment of uncertainty, were imported lock stock and barrel into the two more recent Info-Gap books (Ben-Haim, 2001, 2006) to offer an approach to decision under the severest uncertainty imaginable: "knightian" uncertainty.
To repeat, how can one possibly expect that models designed for the treatment of a mild uncertainty will be suitable for the treatment of "true" Knightian uncertainty!
Indeed, the obove picture speaks for itself. It gives a graphic depiction of the fact that Info-Gap decision theory does not even come close to tackling the severity of the uncertainty that it claims to manage. Info-Gap's formula for dealing with the ("True Knightian") uncertainty that it professes to take on is simply ... to ignore it. This is the effect of Info-Gap prescribing a robustness analysis that fixes only on a given wild guess of the true value of the parameter of interest and its immediate neighborhood, to the exclusion of practically the entire region of uncertainty!
The robustness that one obtains then cannot possibly be declared robustness against severe uncertainty.
All one can say is that the results yielded by the Info-Gap analysis provide a local robustness in the vicinity of a wild guess!
-
And so while it is of course a fact that in his 2001 and 2006 books and in many of his articles, Ben-Haim makes constant reference to Knightian uncertainty, thus giving the impression that Info-Gap is practically tailored to handle this type of forbidding uncertainty; the truth is that Info-Gap constitutes the precise antithesis of what a theory for the treatment of severe uncertainty ought to be.
Because, to repeat, the uncertainty and robustness models deployed by Info-Gap decision theory are the same models deployed in Ben-Haim's 1996 book where the uncertainty under consideration is not assumed to be severe, and where there is no mention of Knightian uncertainty.
- Regrettably, the statement describing the relationship between Ben-Haim's Info-Gap decision theory and Wald's Maximin model which is attributed to my 2008 paper is mistaken and therefore requires a major correction.
In my 2008 paper I set out a detailed proof of a theorem showing that Info-Gap's robustness model is an instance of Wald's Maximin model. That is, I show that the generic Info-Gap robustness model, namely
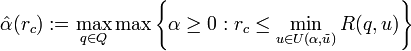
is a simple instance of Wald's generic Maximin model, namely of
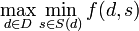
The proof is constructive: it shows that Info-Gap's robustness model is the simple instance of Wald's generic Maximin model specified by
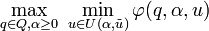
where
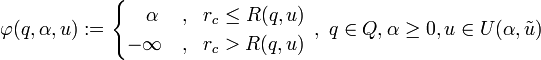
So, the point of this theorem is not that Info-Gap's robustness model is equivalent to Wald's Maximin model. Rather, the point of this theorem is that by virtue of its specific objective function and sets of admissible states, Info-Gap's robustness model constitutes a simple instance of the classical Maximin model. This means, of course, that like countless other instances of Wald's generic Maximin model, the Info-Gap model is subsumed by the Maximin model. The immediate implication is, of course, that Maximin is incomparably more general and powerful than Info-Gap's robustness model so that there can be no talk whatsoever of equivalence between the two models.
Indeed, by analogy, the assertion that Info-Gap's robustness model is equivalent to Wald's Maximin model is as mistaken as the assertion that the family of polynomials specified by
p(x) = 1 + αx2+βx4
is equivalent to the family of polynomials specified by
q(x) = a + bx + cx2+dx3+ex4+fx5+gx6+hx7
or that the class of exponential distributions
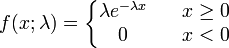
, λ > 0 is equivalent to the class of Weibull distributions
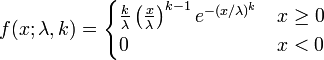
, λ > 0, k > 0 All three assertions share a common feature: they are in error!
- On page 279 the authors formulate the Info-Gap robustness model for decision x, namely

They then go on to argue that this expression shows that their " ... info-gap model is formally at least, equivalent to conventional max-min decision theoretic models (French, 2006) ..."
But, this argument
- Is mistaken. At best it indicates that this particular Info-Gap model is an instance of Wald's generic Maximin model.
- Gives a distorted picture of how the Maximin/info-Gap connection is in fact treated in the Info-Gap decision literature.
- Is far too simplistic to actually capture the kinship between the two models.
To wit:
- Wald's Maximin model is far more general than this Info-Gap model. Indeed, this model is but an instance of Info-Gap's generic robustness model, which in turn is just a simple instance of Wald's generic Maximin model. So how can this model possibly be equivalent to Wald's generic Maximin model??!?!?! It cannot be, and is definitely not, equivalent to Wald's Maximin model.
- There is no reference whatsoever to the fact that Ben-Haim — the Father of Info-Gap — continues to stick to his guns, maintaining his denials that Info-Gap's robustness model is a Maximin model. These denials are made not only in a paper published in the same journal — cited in my 2008 paper — but in other writings and presentations to date, where this question is raised. This includes, among other publications, Ben-Haim's two books on Info-Gap, and his compilation of FAQs about Info-Gap. Also see Review 5 and Review 12.
So, if — as claimed by the authors — the above conclusion follows so directly from the expression describing the above Info-Gap model, shouldn't they have addressed Ben-Haim's persistent claims that Info-Gap's robustness model is not a Maximin model?
- The fact that a "max" and a "min" occur in the formulation of a model does not automatically render this model a Wald's Maximin model. Indeed, to formally show that the above model is a Maximin model it is necessary to reformulate the elements of the model, eg. incorporate the constraint in the objective function of the Maximin model, as done in my 2008 paper.
To illustrate,
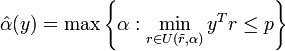
is not a Maximin model, and
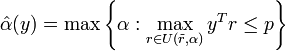
is a Maximin model.
In fact, it is not essential for a model to have an "inner" max or min to be a Maximin model. For instance,
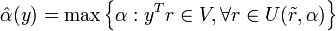
is a perfectly kosher Maximin model.
These subtle modeling issues are discussed and explained in Wikipedia. Also, see my discussion on math formulations of the Maximin model.
- It is no less regrettable that the authors do not address the other fundamental flaws in Info-Gap decision theory — flaws that are described and criticized in detail in my 2007 paper — particularly because these flaws bear directly on the validity of the analysis and results presented in the article.
Specifically, because my arguments (proof and analysis) show that Info-Gap's robustness model fails to tackle the severity posed by the "true" Knightian uncertainty considered in the article — the implications for their analysis and results are obvious.
But, more than anything else, in view of their contention that Info-Gap "is equivalent" to Wald's maximin model, shouldn't the authors have given us at least some indication as to the rationale behind their proposition to use Info-Gap in the first place?!
Shouldn't they have made it clear why, in their view, is there any point, merit, or advantage to turn to Info-Gap rather than stick with the old warhorse Wald's Maximin model, which, one need hardly point out, is the most prevalent model used in the field of "Robust Optimization" and in "Robust portfolio optimization"?!
On the brighter side, though, the authors' statement is a major breakthrough for my Info-Gap campaign. For, after more than three years of hammering this fact, I finally succeeded to convince two dedicated Info-Gap adherents that Ben-Haim's repeated assertions that Info-Gap's robustness model is not a Maximin model are erroneous! (see Review 5).
It is interesting that Ben-Haim still claims that Info-Gap's robustness model is not a Maximin model (see Review 12).
To learn more about the Maximin/Info-Gap connection and Info-Gap's flawed implementation of its Maximin robustness model go to the compilation of FAQs about Info-Gap.


