| Reference: | Yakov Ben-Haim and Scott Cogan |
| Abstract |
We study a 1-dimensional cubic non-linear oscillator in the frequency domain, in which the non-linearity is roughly estimated but highly uncertain. The task is to choose a suite of linear computational models at different excitation frequencies whose responses are useful approximations to, or upper bounds of, the real non-linear system. These model predictions must be robust to uncertainty in the non-linearity. A worst case for the uncertain non-linearity is not known. The central question in this paper is: how to choose the linear computational models when the magnitude of error of the estimated non-linearity is unknown. A resolution is proposed, based on the robustness function of info-gap decision theory. We also prove that the non-probabilistic info-gap robustness is a proxy for the probability of success. |
| Acknowledgements | The authors are pleased to acknowledge useful comments by Lior Davidovitch and Oded Gottlieb. |
| Scores | TUIGF:100% SNHNSNDN:500% GIGO:100% |
Introduction
This is a most intriguing article --- intriguing because its authors are at the forefront of info-gap decision theory. One would have therefore expected them to know better!
Because, the plain fact about the robustness problem studied in this article is that, from the standpoint of robust decision-making, it is manifestly trivial. And what I mean by this is that just looking at this robustness problem you would immediately see that the robustness task is solved by inspection. In other words, it wouldn't even cross your mind to resort to a formal robustness analysis, let alone a local robustness analysis such as the one conducted by info-gap decision theory.
So the question is: what is the point, the merit, the rationale, for using info-gap's "robustness function" to solve this trivial robustness problem seeing that the solution to the global robustness task is immediately obvious by inspection?
The answer to this question is very simple indeed. As in many other info-gap publications, there is no point, or merit, or rationale, for using info-gap's "robustness function" to solve the problem under consideration.
So, let us examine how this fact is manifested in the article under review here.
To do this, the discussion will be conducted under the following headings:
- The wide world of TRIVIAL problems
- You asked for it, you got it!
- Proxy Theorem
- The case of the worst case
- Summary and conclusions
The wide world of TRIVIAL problems
If you strip the problem studied in this article of its "physical" interpretation and you focus exclusively on the underlying robustness problem that it poses, then what you uncover is a simple generic robustness problem consisting of these elements:
- A decision space Q.
- A parameter space U.
- A performance constraint r* ≤ r(q,u)
where r is a real valued function on Q×U and r* is a given numeric scalar.
The robustness question is then as follows:
Robustness question:
How robust is decision q∈Q with respect to the constraint r* ≤ r(q,u) against the variability of u over U?
An intuitive measure of robustness for such problems is the Size Criterion model (circa 1970), according to which the robustness of a decision is measured by the "size" of the subset of U whose elements satisfy the constraints under consideration. So let
A(q):= {u∈U: r* ≤ r(q,u)} , q∈Q
Namely, let A(q) denote the set of "acceptable" values of u pertaining to decision q. This is the subset of U whose elements satisfy the performance constraint for decision q. Naturally, the idea is that the larger A(q) is, the more robust q is. This will be especially justified in situations where these sets are nested, namely if the intersection of any two such sets (for two values of q) is equal to (at least) one of the sets. Observe that this means that one of these two sets is a subset of the other.
Needless to say, to implement the Size Criterion, we must have on hand a suitable means for measuring the "size" of the sets A(q),q∈Q.
But, the whole point about the robustness problem under consideration in this article is that it is so simple (trivial) that the "size" issue is not even an issue, so that the answer to the robustness question literally jumps off the page!
And to see why this is so, consider the following instance of the generic problem considered in the article, namely the case specified by
r(q,u) = f(q) - g(u) , q∈Q, u∈U
where g is a real valued function on U and f is a real valued function on Q.
Note that in this case.
A(q) = {u∈U: r* ≤ f(q) - g(u)} = {u∈U: g(u) ≤ f(q) - r*}
Now.
You may examine this expression any which way you like. But, you cannot possibly avoid this reasoning which essentially answers the robustness question:
Answer to the Robustness Question:
- Clearly, as far as the decision are concerned, the larger f(q) is, the larger A(q) is, hence the more robust q is.
- Hence, f(q) can serve both as a measure of the "size" of A(q) and the robustness of q: the larger f(q) the better.
- The implication is then that the most robust decision is that which maximizes the value of f(q) over q∈Q.
You asked for it, you got it!
The solution to the robustness problem under consideration therefore boils down to this simple recipe:
Recipe for the robustness problem:
- Employ f(q) as a measure of the robustness of decision q.
- Hence rank decisions according to their f(q) values such that the larger the value of f(q), the better.
- The most robust decision is then a decision that is a solution to
max {f(q): q∈Q}
END OF STORY!
Observations:
- The robustness, hence ranking, of the decisions are completely independent of the uncertainty parameter u, the parameter space U and the function g.
- Therefore, the robustness problem is highly "degenerate", hence trivial.
This being so, the question obviously is: what purpose can a local Radius of Stability model (circa 1960) (e.g. info-gap robustness model) serve in this simple case? What is the point in complicating the analysis by introducing an estimate and a neighborhood structure on the uncertainty space U around this estimate?
None
And yet, the authors foist on this trivial robustness problem a local robustness analysis, using to this end the following Radius of Stability model:
α(q,û):= max {α≥0: r* ≤ r(q,u), ∀u∈U(α,û)} , q∈Q
where û is a point estimate of the true value of u and U(α,û) denotes a neighborhood of radius α around û.
Here α(q,û) denotes the Radius of Stability of decision q at û. It is the radius of the largest neighborhood U(α,û) all whose elements satisfy the constraint r* ≤ r(q,u) for decision q. Equivalently, it is the radius of the largest neighborhood U(α,û) that is contained in A(q).
Observe that for the trivial case considered in the article, namely r(q,u) = f(q) - g(u), this local model takes the following form
α(q,û) = max {α≥0: r* ≤ r(q,u), ∀u∈U(α,û)} = max {α≥0: r* ≤ f(q) - g(u), ∀u∈U(α,û)} = max {α≥0: g(u) ≤ f(q) - r*, ∀u∈U(α,û)} = max {α≥0: max {g(u): u∈U(α,û)} ≤ f(q) - r*}
Since the neighborhoods are nested, namely α' < α" implies that U(α',û)⊆U(α",û), it follows by inspection that α(q,û) is non-decreasing with f(q).
In short, f(q) can also be used as a measure of local robustness (assuming, with no loss of generality that r* ≤ r(q,û),∀q∈Q).
So, what merit can there possibly be to using the far more complicated local Radius of Stability model rather than the very simple (indeed, in this case, trivial ) Size Criterion model?
And to make this point patently clear, here are the two approaches, side by side:
| Model | info-gap | Size Criterion |
| robustness of decision q | max {α≥0: max {g(u): u∈U(α,û)} ≤ f(q) - r*} | f(q) |
| decision problem | maxq∈Qmax {α≥0: max {g(u): u∈U(α,û)} ≤ f(q) - r*} | max {f(q): q∈Q} |
The following observation provides further evidence of how alien the neighborhoods U(α,û), α≥0, are in the robustness analysis of the problem featured in the article:
Consider the (quite common) case where U(α,û) is strictly increasing (set-inclusion-wise) with α. Then clearly, in this case the structure of the neighborhoods U(α,û), α≥0, has no impact whatsoever on the ranking of the decisions. The definition of these sets only affect the "distance" of the elements of U from the estimate û. In other words, the definition of these sets affects the values of the radii of stability of the decisions, but not their ranking (robustness-wise).
That said, I should point out that it is also important to note that the article is mum on the fact that the local robustness model proposed in this article for the treatment of the trivial robustness problem in question, is a simple Radius of Stability model. Neither does it make clear, that Radius of Stability models have been used extensively in many fields for the purpose of local robustness analysis, since the 1960's. Nor indeed, that there is a huge literature on the stability of matrices and polynomials associated with dynamical systems (see reference below to Hinrichsen and Pritchard seminal work in this area).
And what is most interesting of all, is that in the analysis of the "Proxy Theorem", the authors do use the ... Size Criterion.
Proxy Theorem
Having said all that, let us now examine the authors' dramatic declaration in the abstract: "We also prove that the non-probabilistic info-gap robustness is a proxy for the probability of success."
Because, the question arising is this: What exactly have the authors proved through their solution of a trivially simple problem, using for the purposes of this exercise info-gap's "robustness function"?
They proved that: if you are dealing with an exceedingly trivial case, you stand to obtain the momentous result that in this trivial case "...the non-probabilistic info-gap robustness is a proxy for the probability of success ...". Surely, this should have been obvious to begin with!
Because, observe that even a superficial examination immediately reveals that:
- Since f(q') < f(q") implies that A(q') ⊆ A(q"), it follows that regardless of what probability structure is imposed on U, the probability that u is in A(q') is not greater than the probability that u is in A(q").
- Therefore, ranking decisions according to their f(q) values is the same as ranking decisions according to their "probability of success".
In other words, the ranking of decisions is invariant with the probability structure imposed on the parameter set U which is an immediate indication of how trivial the problem under consideration is:
The probability structure on U has no impact whatsoever on the ranking of the decisions according to their global robustness with respect to the constraint r* ≤ r(q,u)!!!Surely, this can only mean that the problem under consideration must be highly "degenerate", hence downright trivial. For, in what other case (other than a trivial one) would the ranking of decisions according to their robustness on U with respect to r* ≤ r(q,u) be totally independent of the probability distribution of u?
So, all that's left to say about the result "...the non-probabilistic info-gap robustness is a proxy for the probability of success ..." is: what is the wonder?!! If you pose a trivial problem, chances are that the solution to this trivial problem will be trivially simple!
And this further underscores the question raised above: what advantage can there possibly be in complicating the analysis by introducing an info-gap robustness model into the picture?
What do we stand to gain from foisting on the above exceedingly simple analysis two rather complicated info-gap models such as these?
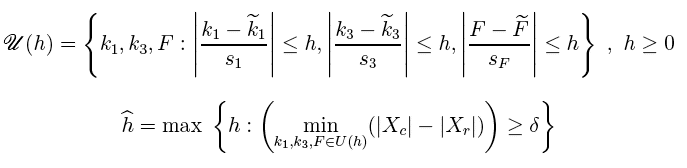
The first is the neighborhood structure proposed in the article and the second is the associated info-gap robustness model.
Suffice it to say that in these models h represent the horizon of uncertainty (α); Xc represents function f; |Xr| represents function g; (k1,k3,F) represents u; and δ represents r*. Decision q is represented by three parameters that are not shown explicitly in these models (formally they are implicit arguments of |Xc|).
And to shed more light on the Proxy Theorems issue, I want to point out the following.
On page 12 of the article we read:
In this section we discuss a theorem which asserts that the non-probabilistic info-gap robustness is monotonically related to the probability that the non-linear system satisfies the performance requirement. This 'proxy property' is important since, when it holds, it implies that a computational model can be chosen which maximizes the probability of success, without knowing the probability distribution of the uncertain variables. The value of maximum probability will remain unknown.
It is important to take note then that, as stated very clearly in Davidovitch's (2009), proxy theorems are expected to be "very rare":
We have shown that the definition of strong proxy theorems discussed by Ben-Haim (2007), is very restrictive, and that when the uncertainty is multi-dimensional, strong proxy theorems are expected to be very rare. Then we shall prove that even this weaker definition does not hold for a wide family of common problems.
Davidovitch (2009, p. 137)
PhD Thesis, Department of Mechanical Engineering, Technion
Since the technical issues are discussed in detail in Davidovitch (2009), I shall not elaborate on them here.
I should, however, call attention to the following important issue that is not discussed in Davidovitch (2009) --- nor in Ben-Haim (2007):
The whole point about info-gap "Proxy Theorems" is that they typically hold for .... trivial robustness problems. This is so because these theorems impose extremely limiting requirements on the elements of the robustness model such that invariably simplify the global robustness problem under consideration to the point of rendering it trivial.
As we just saw, trivial problems of this type can be solved without any appeal to a local model of robustness such as info-gap's robustness mode. Differently put, such a model only complicates an otherwise trivial robustness analysis.
The bottom line is then that info-gap scholars are yet to identify a non-trivial robustness problem that would benefit from existing Proxy Theorems. I undertake to immediately post such a problem on this page.
And this leads me straight to an examination of a number of cryptic statements made in this article about worst-case.
The case of the worst case
To emphasize info-gap's purported unique ability to deal with severe uncertainty, the article repeatedly calls attention to the fact that the horizon of uncertainty α is unbounded (above). But in their zeal to underscore this fact, the authors obscure the relation between worst-case analysis and info-gap's robustness analysis. Thus, in the abstract of the article we read:
The worst case for the uncertain non-linearity is not known.
Then, in page 4 we read
Moreover, we assume that a worst case for this uncertainty is not known
And in page 6:
These error estimates do not constitute knowledge of a worst case.
And in page 8:
Since we do not know the magnitude of error --- no realistic worst case is known --- the horizon of uncertainty is unbounded.
And in page 14:
It is assumed that the worst case for the uncertainties is not known.
My point is then that these statements --- which incidentally are of a piece with similar statements in the info-gap literature, including the three primary texts (Ben-Haim 2001, 2006, 2010) --- not only obscure the fact that info-gap's robustness analysis is indeed a (local) worst-case analysis, but that info-gap's robustness model is in fact a simple Maximin model.
The important point to note here is that the worst-case analysis conducted by info-gap decision theory is local rather than global. That is, the important point here is that info-gap's worst case analysis is not conducted on the parameter space U. It is conducted, for each α ≥ 0, only on the neighborhood U(α,û), namely in the neighborhood of radius α around the estimate û. It therefore follows that the fact that α is unbounded above has no bearing whatsoever on the fact that a worst-case analysis is conducted for each value of α on the neighborhood U(α,û), namely in the neighborhood of radius α around the estimate û.
But more than this, info-gap's worst case analysis is conducted with respect to a constraint. This means that a worst case always exists. In other words, there are at most two cases: either the constraint is satisfied or it is violated. Since there are at most two "cases", there is always a worst case (even if α is unbounded).
I should add that the big fuss that is being made in info-gap publications about the fact that the horizon of uncertainty α is allowed to be unbounded (above) in fact borders on the risible. As those who are familiar with this literature would no doubt know, the momentous point that is supposed to be made by these repeated assertions is that an info-gap model is capable of dealing with the severest uncertainty. One imagines therefore that this is the rationale for the repeated assertions that an info-gap model does not posit a worst-case. Presumably, given that the horizon of uncertainty α is unbounded (above), there would not be a worse case.
What is so amusing about these repeated assertions is that for all the song and dance about the horizon of uncertainty α being unbounded (above), when it comes to conducting the robustness analysis itself, the whole business of the horizon of uncertainty α being unbounded (above) comes to naught! Because, what does info-gap decision theory prescribe doing? It prescribes conducting a worst-case analysis only on the neighborhood U(α,û), for one given α at a time, namely in the neighborhood of radius α around the estimate û. So, methodologically speaking, it does not make one jot of difference whether the horizon of uncertainty α is bounded or unbounded.
And to further illustrate this point, keep in mind that the objective of info-gap's robustness model is to .... maximize the value of α. That is:
So, at first glance you would no doubt ask:
How can one possibly maximize the value of α if --- as claimed by the authors --- α is unbounded above?
The answer to this question is simplicity itself. This apparent contradiction does not even arise when you realize that the whole point about info-gap's robustness analysis is that regardless of whether α is or is not unbounded above, info-gap's robustness analysis is driven by the robustness constraint. Thus, in the info-gap robustness analysis, the robustness constraint r* ≤ r(q,u),∀u∈U(α,û) prevents the admissible values of α from increasing indefinitely. Consequently, the robustness of decision q is the largest admissible value of α with respect to the performance constraint imposed on q.
So much then for the purported merit of the horizon of uncertainty α being unbounded above!
And as a final note about the worst-case issue, I should point out the following. What is truly remarkable about the repeated (implicit) denials in this article that info-gap's robustness analysis is a worst-case analysis is that .... in a number of papers by Hemez and Ben-Haim (2002, 2003, 2004), the precise opposite is maintained. Indeed, these papers state categorically that info-gap's robustness analysis is ... a worst case analysis (see Review 23, Review 23, Review 25 ).
For instance, the caption to Figure 6-2 in Hemez, Ben-Haim, and Cogan (2002) reads as follows (emphasis added):
Worst-case info-gap robustness.
And in Hemez and Ben-Haim (2003, p. 10) we read (emphasis added):
For the application, the optimization searches for the model that yields the worst possible test-analysis correlation metric R(q;u) at each uncertainty level.
And the caption to Figure 7 in Hemez and Ben-Haim (2004) reads as follows (emphasis added):
Results of the worst-case info-gap robustness analysis.
Indeed, is it possible to hold otherwise? Because, take a look at info-gap's generic robustness model:
Clearly the ∀u∈U(α,û) clause indicates in no uncertain terms that a worst-case analysis is conducted on the premises: all the values of u∈U(α,û) must satisfy the constraint --- hence also the worst u∈U(α,û). Conversely, if the worst u∈U(α,û) satisfies the constraint, then so do all the other elements of U(α,û).
In short, the "worst case" story is as follows:
Beginning of Story.
For each α≥0, one at a time, a worst case analysis of the constraint r* ≤ r(q,u) is conducted on U(α,û).
End of Story.
And for a second opinion on this issue --- keeping in mind that info-gap's robustness model is a simple Radius of Stability model --- consider the following statements (emphasis added):
We then introduce the stability radius as a measure of the smallest perturbation for which the perturbed system no longer satisfies the constraints. This is a worst case robustness measure expressed by a single number that provides an efficient tool for assessing the robustness of the stability of a given system.
Hinrichsen, and Pritchard (2005, p.519)The stability radius is a worst case measure of robustness. It measures the size of the smallest perturbation for which the perturbed system is either not well-posed or does not have spectrum in Cg.
Hinrichsen and Pritchard (2005, p. 585)
And just in case you are not familiar with Hinrichsen and Pritchard's (1986, 2005) seminal work on the Radius of Stability in the field of control theory, consider this:
Robustness analysis has played a prominent role in the theory of linear systems. In particular the state-state approach via stability radii has received considerable attention, see [HP2], [HP3], and references therein. In this approach a perturbation structure is defined for a realization of the system, and the robustness of the system is identified with the norm of the smallest destabilizing perturbation. In recent years there has been a great deal of work done on extending these results to more general perturbation classes, see, for example, the survey paper [PD], and for recent results on stability radii with respect to real perturbations.
Paice and Wirth (1998, p. 289)
here: HP2 = Hinrichsen and Pritchard (1990), HP3 = Hinrichsen and Pritchard (1992) and PD= Packard and Doyle (1993).
So much then for the worst case issue.
Summary and conclusions
The obvious conclusion to be drawn from this short discussion is that the info-gap decision model, proposed by the authors for the solution of the trivially simple problem studied in this article, is at best redundant.
Because, consider what this article accomplishes.
Granting that the objective here is to illustrate the capabilities of info-gap's "robustness function", then all that this article does is to demonstrated the sledgehammer approach: how to solve a trivially simple problem by means of an unduly complicated model/procedure.
The trouble is, though, that this proposition not only contributes nothing to our understanding of the robustness problem examined in the article. It actually obscures from view how trivially simple this problem really is. Hence, how trivially simple its solution is!
And the greater trouble is that analysts, practitioners etc. who are not versed in decision theory, optimization theory, and related areas of expertise, may not be able to evaluate and judge these propositions for what they are!
And this remark leads me straight to comment on the distorted view that this article gives of the state of the art. Because, readers who are not versed in decision theory, optimization theory, robust optimization, control theory, etc. may not be able to tell that what is truly absent from this article are the basic facts about info-gap decision theory.
The missing links
The real facts about info-gap decision theory and the analysis presented in Ben-Haim and Cogan (2011) are these:
- Info-gap's robustness model is a simple Radius of Stability model (circa 1960).
- Info-gap's robustness model is a simple instance of Wald's famous Maximin model (1939).
- Info-gap's robustness model is a model of local robustness. It is therefore utterly unsuitable for the treatment of severe uncertainty.
- Info-gap Proxy Theorems are extremely rare (Davidovitch 2009). Typically, they would be associated with trivial robustness problems such as the one featured in Ben-Haim and Cogan (2011).
- Not a single hint (references) is given in Ben-Haim and Cogan (2011) to the fact that Radius of Stability issues of the type discussed in this article have been the subject of extensive research in areas such as applied mathematics, numerical analysis, control theory, etc. The authors are encouraged to take a quick look at Hinrichsen and Pritchard's (2005) book Mathematical systems theory I: modelling, state space analysis, stability and robustness).


