| Reference: |
Brendan A. Wintle, Michael C. Runge and Sarah A. Bekessy Allocating monitoring effort in the face of unknown unknowns Ecology Letters, (2010) doi: 10.1111/j.1461-0248.2010.01514.x |
| Abstract | There is a growing view that to make efficient use of resources, ecological monitoring should be hypothesis-driven and targeted to address specific management questions. Targeted monitoring has been contrasted with other approaches in which a range of quantities are monitored in case they exhibit an alarming trend or provide ad hoc ecological insights. The second form of monitoring, described as surveillance, has been criticized because it does not usually aim to discern between competing hypotheses, and its benefits are harder to identify a priori. The alternative view is that the existence of surveillance data may enable rapid corroboration of emerging hypotheses or help to detect important unknown unknowns that, if undetected, could lead to catastrophic outcomes or missed opportunities. We derive a model to evaluate and compare the efficiency of investments in surveillance and targeted monitoring. We find that a decision to invest in surveillance monitoring may be defensible if: (1) the surveillance design is more likely to discover or corroborate previously unknown phenomena than a targeted design and (2) the expected benefits (or avoided costs) arising from discovery are substantially higher than those arising from a well-planned targeted design. Our examination highlights the importance of being explicit about the objectives, costs and expected benefits of monitoring in a decision analytic framework. |
| Keywords | Adaptive management, cost efficiency, decision theory, Knightian uncertainty, surprise, surveillance. |
| Acknowledgments | This work arose in conversation with participants of the Applied Environmental Decision Analysis (AEDA) working group on optimal monitoring. We make particular acknowledgement of the contributions of Yohay Carmel, Yakov Ben-Haim, Clare Hawkins, Adrian Manning, Mark Antos, Mark Burgman and Hugh Possingham. We are grateful to Jim Nichols and Georgia Garrard for comments on an earlier draft. Reviews by Nigel Yoccoz, Jonathan Rhodes and two anonymous referees substantially improved the manuscript. BW and SB were supported by ARC grants DP0774288 and LP0882780, and the Commonwealth Department of Environment, Water, Heritage and the Arts via AEDA. MR was supported by AEDA, the Australian Centre for Excellence in Risk Analysis and the US Geological Survey. |
| Scores | TUIGF:100% SNHNSNDN:100% GIGO:9998% |
There is a story about this article in Decision Point # 43, 2010, pp. 4-7.Overview
There are known knowns
there are things we know that we know.
There are known unknowns;
that is to say, there are things that we
now know we don’t know.
But there are also
unknown unknowns;
there are things we do not know we don’t know.
This is an extremely interesting article, but not necessarily for its info-gap content.Rather, the interest in this article lies in its proposed treatment of one of the most daunting problems facing mankind, namely the question of how to deal with problems involving unknown unknowns. This is the first publication on this topic that I have ever come across which practically outlines a methodology for solving this onerous problem.
The recipe that the authors provide is too good to be true: All that is required for this purpose is a "... a blend of standard statistical approaches and expert-elicited estimation or bounding ..." and, of course, a doze of info-gap decision theory.
I address the following points, noting that only the first three are related to info-gap decision theory per se:
- Relation between info-gap decision theory and Wald's Maximin model (circa 1940).
- Invariance Property of info-gap's robustness model (2007).
- Knight's distinction between Risk and Uncertainty (1921).
- Taleb's Black Swans (2007).
- Proposed treatment of unknown unknowns.
- How do you catch a red koala?
Info-gap decision theory
First, a general comment.
It is hard to comprehend why info-gap enthusiasts continue to cling to a debunked theory, especially to its phraseology and rhetoric, when they should be well aware that these have been shown to be erroneous and misleading.
It seems therefore that info-gap enthusiasts will, for the time being, require constant reminding of the true nature of the Maximin/info-gap robustness model connection. Specifically, they will need reminding that info-gap's robustness model is a simple instance of Wald's Maximin model.
Likewise, they will require, for the time being, constant reminding that info-gap's robustness model is a model of local robustness, known universally as radius of stability model. Therefore, by virtue of its design, it does not, much less can it, "explore" the entire assumed uncertainty space. All it can do, by definition, is "explore" small perturbations in the value of the estimate.
The reason that it is important to keep on hammering these simple facts is not only to bring info-gap adherents to, as it were "see the light", but to alert readers of publications dealing with info-gap decision theory, or indeed just referring to it, that this is a fundamentally flawed theory. For one thing, it is important to alert, especially those readers who are not conversant with decision theory, optimization theory, etc., that the phraseology and rhetoric in publications discussing info-gap decision theory's nature, capabilities, and so on, are grossly misleading. It is important to call these readers' attention to the fact that the info-gap phraseology and rhetoric have little in common with what info-gap decision theory actually is and does. I should perhaps also remind readers that articles published in peer-reviewed journals can be profoundly flawed, misleading, etc.
And now to the article itself.
The Maximin connection
First, the references in the article to info-gap decision theory and Wald's Maximin model:
Page 8:
The third type of model application would involve a formal uncertainty analysis that explores the full space of monitoring investment options and parameter uncertainties to identify the most robust monitoring investment (sensu Wald 1945, Ben-Haim 2006).
Page 11:
The magnitude of uncertainty surrounding most of the model parameters demands that the model be utilized within a sound uncertainty analysis framework. Relevant approaches might include (but are not limited to) robust optimization, maxi–min or info-gap decision theories (Wald 1945; Ben-Tal & Nemirovski 2002; Ben-Haim 2006).
The reason that I call attention to these statements is to make it clear that however innocuous their reference to info-gap's robustness model and to Wald's Maximin model, the manner in which they refer to these two models can easily give the wrong impression about the true relation between the two models. These statements clearly do not indicate that info-gap's robustness model is a simple instance of Wald's Maximin model. Worse, they may easily be construed as suggesting that the two models are on a par. So, readers of this article take note: info-gap's robustness model is a simple instance of Wald's Maximin model. Show/hide a larger version of the proof.
As for the claim made in the first statement regarding the capabilities of info-gap's robustness model. As I explain in the following section, this claim is downright false. Info-gap's robustness model (Ben-Haim 2006) does not, much less can it, "explore" the full uncertainty space. This is so for the simple reason that for each decision (monitoring investment), it "explores" only the region of uncertainty around an estimate whose size is equal to the robustness of the decision, namely the radius of stability of the decision.
Invariance property and No Man's Land syndrome
To reiterate, the assertion that info-gap's robustness model "explores" the entire uncertainty space is manifestly wrong because info-gap's robustness model is a radius of stability model. As such a model it can "explore" only the immediate neighborhood of an estimate. Namely, it explores only the ball centered at the estimate whose radius is equal to the distance of the estimate to the region of instability (region where the performance requirement is violated).
In the language of info-gap decision theory, for each decision, info-gap's robustness model "explores" only the neighborhood of the estimate that is within a certain distance from the estimate. This distance is equal to the robustness of the decision. So, except for the trivial case (where a decision satisfies the performance requirement over the entire uncertainty space), that is where the question of robustness does not arise, this model does not explore the entire uncertainty space as such.
To put it differently:
- Info-gap decision theory does not seek decisions that are robust against severe uncertainty.
- Info-gap decision theory seeks decisions that are robust against small perturbations in the nominal value of a parameter of interest.
In any case, I refer to this property of info-gap's robustness model as the Invariance Property and I appeal to it to explain, formally, why info-gap decision theory is utterly unsuitable for the treatment of severe uncertainty.
The picture is this:
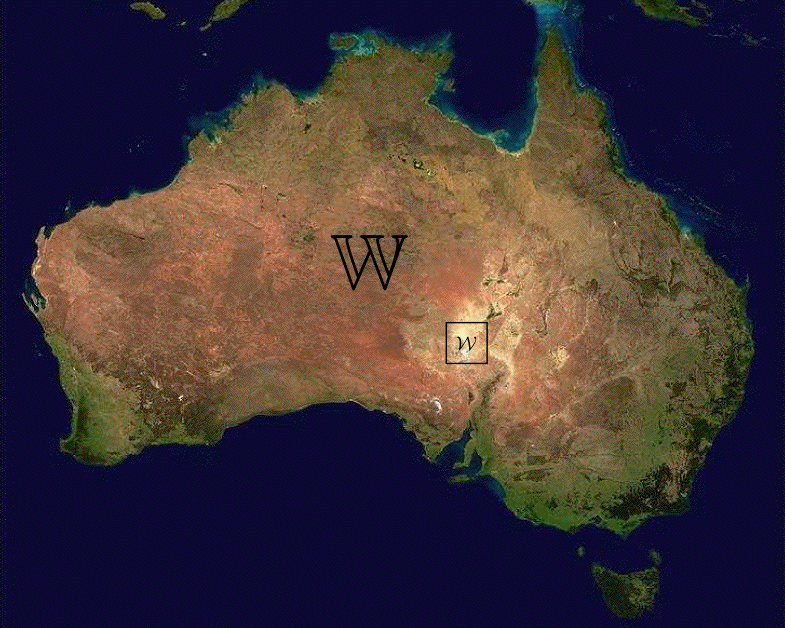
This is a bird's view of info-gap decision theory's approach to severe uncertainty. The uncertainty space W is represented by the island, and the sample space w by the area surrounding Elliot Price Conservation Park (The small whitish area is Lake Eyre). The picture is a NASA satellite image of Australia. See WIKIPIDIA at http://en.wikipedia.org/wiki/File:Australia_satellite_plane.jpg.
The objective of this picture is to make vivid info-gap's (absurd) central proposition. The prescription it puts forward for the modeling/mangement of severe uncertainty is to focus the robustness analysis of a decision only over the small square w. It then goes on to contends that a decision that is deemed robust (fragile) with respect to the small area in the middle of the island (w), is also robust (fragile) with respect to the entire island (W).
In the language of info-gap decision theory, the small area (w) consists of all the points in W whose distance from the estimate is not greater than the robustness of the decision under consideration. In the language of stability theory, w is the ball whose radius is equal to the radius of stability of the decision at the estimate.
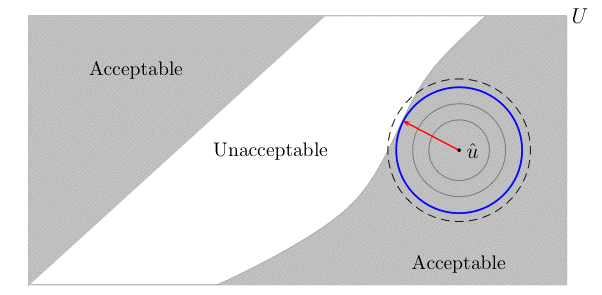
For the benefit of readers who are not familiar with info-gap decision theory, here is a more edifying picture:
The large rectangle (U) represents the uncertainty space under consideration, the shaded area represents the points where the decision under consideration satisfies the performance requirement. The dot (û) represents the estimate and the bold blue circle represents the region of uncertainty around the estimate whose radius is equal to the robustness of the decision. Note that the radius of the circle (info-gap robustness) is not affected by the performance of the decisions at points that are distant from the circle. That is, the area outside the dashed circle is an info-gap No Man's Land: the performance of the decision outside this area has no impact whatsoever on the robustness of the decision.
So, the question is on what grounds do the authors claim that info-gap decision theory "explores" the entire uncertainty space?
Clearly, the obvious conclusion to be drawn from this illustration is that, methodologically hence practically, info-gap's robustness model does not "explore" the entire uncertainty space, except in the trivial case where robustness is not an issue. Namely, in cases where a decision satisfies the performance requirement over the entire uncertainty space. To put it more bluntly, as shown above, in virtue of its definition , info-gap's robustness model is oblivious to the performance of a decision outside the region of uncertainty determined by the robustness of the decision, meaning that effectively it does not care a straw about the entire uncertainty space. This is precisely what makes info-gap an utterly unsuitable method for severe uncertainty.
Knightian Uncertainty
According to the authors (p. 2):Knight's (1921) three part typology has been enormously influential to modern decision theory: certainty governs the case when the deterministic outcomes of all alternative actions are known; risk forms the basis of normative decision theory, and describes a decision context in which the outcome is stochastic, but the contingencies and their probabilities are known; and uncertainty concerns the case of severe uncertainty under which the probabilities (or probability distributions) of a set of known contingencies are unknown (e.g. Ben-Haim 2006).But, this is an inaccurate reading of Knight's conception of uncertainty. As attested by Knight's own explanation, uncertainty is in fact a broader, more general concept encompassing also "unknown unknowns". Thus, contrary to common interpretations of Knight's notion of uncertainty, his own explanation makes it plain that uncertainty subsumes unknown "instances" or "contingencies" such that it is impossible to specify what they might be. In Knight's (1921, III.VIII.2) own words (emphasis is mine):
The practical difference between the two categories, risk and uncertainty, is that in the former the distribution of the outcome in a group of instances is known (either through calculation a priori or from statistics of past experience), while in the case of uncertainty this is not true, the reason being in general that it is impossible to form a group of instances, because the situation dealt with is in a high degree unique. The best example of uncertainty is in connection with the exercise of judgment or the formation of those opinions as to the future course of events, which opinions (and not scientific knowledge) actually guide most of our conduct.In other words, according to Knight, the concept uncertainty also represents situations where the uncertainty space itself can be partially or completely unknown, in which case we are dealing with "unknown unknowns".
Be that as it may, the point that must be made clear to readers of this article and more generally to readers of the info-gap literature, is the following. The terms "Knightian uncertainty" or, "True Knightian uncertainty", are used with abandon in the info-gap literature to signify the daunting, forbidding uncertainty -- manifested in poor estimates and vast (indeed unbounded) uncertainty spaces -- that info-gap decision theory is claimed to take on. Recall Ben-Haim's claim (2006, p. 210) that the most commonly encountered info-gap models of uncertainty have unbounded uncertainty spaces.
But the truth of the matter is that info-gap decision theory is utterly incapable of taking on this task. This fact is amply demonstrated by the Invariance Property. The trouble is, however, that the phraseology and rhetoric in publications on info-gap decision theory, or publications merely refering to it, give readers the wrong impression that info-gap decision theory is designed precisely for this type of uncertainty. So, to repeat, readers of this article take note: info-gap decision theory is, as a matter of principle, incapable of handling Knightian uncertainty, "true knightian uncertainty", "Unknown unknowns" or any other "real" uncertainty.
Black Swans
It is also important to correct the authors' reference to Naseem Taleb's concept of Black Swan which they lump together with other conceptions of uncertainty in their discussion on "unknown unknowns" (page 2, emphasis is mine):
Genuine surprise (Hilborn 1987) goes beyond the conventional interpretation of Knightian uncertainty to encompass the case in which both the contingencies and (by definition their probabilities) are unknown. Such uncertainties are called unknown unknowns or black swans in popular parlance (Furlong 1984; Rumsfeld 2002; Taleb 2007) and are considered by some to be the most important uncertainties in our lives (Taleb 2007). Particularly in the face of global climate change, there is considerable concern about how to be open to surprise and seek discovery of unforeseen phenomena (e.g. Schneider et al. 1998).This is a huge misrepresentation of the idea of the Black Swan. Because, according to Taleb (pp. xvii-xviii):
What we call here a Black Swan (and capitalize it) is an event with the following three attributes.
First, it is an outlier, as it lies outside the realm of regular expectations, because nothing in the past can convincingly point to its possibility. Second, it carries an extreme impact. Third, in spite of its outlier status, human nature makes us concoct explanations for its occurrence after the fact, making it explainable and predictable.
I stop and summarize the triplet: rarity, extreme impact, and retrospective (though not prospective) predictability. A small number of Black Swans explains almost everything in our world, from the success of ideas and religions, to the dynamics of historical events, to elements of our own personal lives.
That is, according to Taleb (2007), "Black Swans" are not just highly (you might say, in principle) unpredictable events. Eliminate one ingredient from the triplet and you no longer have a "Black Swan".
Still, I am not going to pursue these inaccuracies any further as the main aim of this review is to concentrate on one of the central concerns in this paper. This is the proposed strategy, outlined in this article, for dealing with phenomena, occurrences, etc., captured by the phrase "unknown unknowns".
Unknown Unknowns
For the benefit of readers who are not familiar with this concept, here is the opening paragraph of the entry "unknown unknown" in Wikipedia:
In epistemology and decision theory, the term unknown unknown refers to circumstances or outcomes that were not conceived of by an observer at a given point in time. The meaning of the term becomes more clear when it is contrasted with the known unknown, which refers to circumstances or outcomes that are known to be possible, but it is unknown whether or not they will be realized. The term is used in project planning and decision analysis to explain that any model of the future can only be informed by information that is currently available to the observer and, as such, faces substantial limitations and unknown risk.It is immediately clear that the challenge presented by decision problems involving "unknown unknowns" is enormous. Yet, the authors appear undaunted by the enormity of the task, and they boldly proceed to outline a quantitative model aimed at solving problems involving "unknown unknowns" that arise in the context of a combined targeting-surveillance monitoring system. And what is more, they unhesitantly recommend the strategy outlined in the article as the basis for "any monitoring program". So the question is: Does this article report on a major breakthrough in decision-making under severe uncertainty?
The answer, of course, is that a cursory examination suffices to reveal that the model proposed for the treatment of "unknown unknowns" in the framework of a combined targeting-surveillance monitoring system, is in fact a chimera. Its central proposition is untenable because it is based on a self-contradiction.
Proposed methodology for the treatment of unknown unknowns
In a nutshell, the proposed methodology is based on the proposition that it is somehow possible to transform an "unknown unknowns" problem into an equivalent "known unknowns" problem by estimating the properties of interest of the "unknown unknowns" under consideration.
The fact, of course, is that by definition, "unknown unknowns" are imponderable: We have no clue "who they are", "what they are", "when they will appear on the scene" etc. By necessity, therefore, we cannot reliably compute the expected cost/benefits associated with their appearance on the scene, the cost averted by discovering them, etc. Yet, inexplicably this is not a real issue in this article!
For consider what the model of the proposed methodology requires doing. The model calls for, among other things, the following parameters (page 5):
" ... Each of these programs has a probability pi of discovering an unforeseen pattern, given the pattern occurs, ..."and" ... C is the cost averted by discovering (and ameliorating) a novel threat (an unknown unknown) ..."and" ... Finally, we have an a priori belief that an unforeseen pattern will emerge with probability f, the background frequency with which unforeseen disasters occur ... "where the terms "unforeseen pattern", "a novel threat", and "unforeseen disasters" represent "unknown unknowns".
If you ignore the rhetoric and focus on the proposed model itself, you discover that these "unknown unknowns" are treated exactly like "known unknowns". So much so that it is unclear in what sense are these supposed "unknown unknowns" genuine "unknown unknowns". After all, they look like "known unknown", they behave like "known unknown", and they are handled in the proposed formal model as if they were "known unknowns".
Let us then examine the proposed model:
known unknows unknown unknowns V(v) = R[1-(1-q1(v))(1-q2(B-v))] − fC[(1-p1(v))(1-p2(B-v))]
B = total budget. v = amount of budget units allocated to the targeted monitoring program (0 ≤ v ≤ B). R = reward gained from improvements to management arising from better knowledge or understanding of the known unknowns. C = cost averted by discovering (and ameliorating) the unknown unknowns. q1(x) = probability of achieving management benefit from the targeted-monitoring program (detecting known unknowns) given that x units of the budget are allocated to this program (0 ≤ x ≤ B). q2(x) = probability of achieving management benefit (detecting known unknowns) from the surveillance-monitoring program given that x units of the budget are allocated to this program (0 ≤ x ≤ B). p1(x) = probability of discovering the unknown unknowns by the targeted monitoring program, given that they occur and that x units of the budget are allocated to this program (0 ≤ x ≤ B). p2(x) = probability of discovering the unknown unknowns by the surveillance-monitoring program, given that they occur and that x units of the budget are allocated to this program (0 ≤ x ≤ B). f = background frequency (probability) with which unknown unknowns occur. In case the obvious flaw in the proposed methodology is not immediately clear to you, ask yourself the following questions.
- How would we compute the cost averted by discovering a novel "unknown unknown" threat (C)? And how would we compute the probability that a monitoring program will discover an "unknown unknown" threat, should it occur (p)? Indeed, how are we going to compute the probability/likelihood that an "unknown unknown" threat will occur in the first place (f)?
- Doesn't the fundamental difficulty in dealing with genuine "unknown unknowns" come down precisely to this: We have no clue how to compute costs/benefits pertaining to them (C), nor how to compute the probability that they will be discovered by a given monitoring program should they occur (p), nor how to compute the probability that they will occur (f)?
- In what way is quantifying the parameters (R,q) of the "known unknown" different from quantifying the parameters of the "unknown unknowns" (C,p,f)?
So as we can clearly see, for the authors the fundamental difficulty associate with "unknown unknown" is not an issue. They resolve it by simply prescribing that we ... assume that we know all we need to know about these "unknown unknowns", namely the values of C, p, and f.
To which I say:
- If you can compute a reliable estimate of the cost/benefit (C) associated with IT; and
- If you can compute a reliable estimate of the probability that IT will be discovered should it occur (p); and
- If you can compute a reliable estimate of the probability that IT will occur (f),
then
- that IT -- whatever it is -- is ain't an "unknown unknown"!
The proposed methodology reminds me of an old puzzle.
How do you catch a red koala?
Catching a red koala is not as difficult a task as you may have thought at first. In fact, here is a tested, fool-proof algorithm for this task.
Algorithm for catching a red koala:
- Step 1: Catch a koala, any koala.
- Step 2: If it is red, STOP! Otherwise, go to the Step 3.
- Step 3: Paint it red.
- Step 4: STOP!
This is roughly the type of recipe that the authors propose for the treatment of "unknown unknowns". Because, for all the talk early on in the discussion about the forbidding nature of "unknown unknowns", this is what we read on page 9:
Estimation of the parameters of our model will require a blend of standard statistical approaches and expert-elicited estimation or bounding.and later onThe most difficult parameters in our model to estimate are the parameters of surprise: the expected frequency of unforeseen ecological patterns or phenomena, the costs of those surprises, and the probability of discovering them with a given monitoring design (f, C, pi). By definition, surprises about ecological phenomena are not predictable and their impacts cannot be known a priori. However, that does not mean that the historical rate at which surprises occur cannot be observed and estimated, especially given some careful bounding of the problem.The mind boggles reading this.
Described schematically, the authors' prescription for the solution of the daunting "unknown unknowns" problem boils down to this:
- Step 1: Transform the "unknown unknowns" under consideration into "known unknowns".
- Step 2: Solve the associated, much simpler, "known unknowns" problem.
Apparently, the first step is no big deal, as it involves no more than the use of a ".... blend of standard statistical approaches and expert-elicited estimation or bounding ..."
One wonders whether it occurred to the authors to ask themselves the following question: Given that the treatment of "known unknowns" often requires the use of a ".... blend of standard statistical approaches and expert-elicited estimation or bounding ...", in what way, if any, are "unknown unknowns" treated by our (one ought to add extremely general) model, differently than "known unknowns"?
And hadn't it occurred to them that pursuing this logic they could have just as well watered down Knight's distinction between "risk" and "uncertainty", by simply invoking a ".... blend of standard statistical approaches and expert-elicited estimation or bounding ..." to construct a (subjective) probability distribution or some other likelihood structure, on the uncertainty space?
In short, the most striking thing about this article is its total blurring of the lines between "known unknowns" and "unknown unknowns".
Quality Control
The reason that the authors did not realize that their proposed method is based on a blurring of the lines between "unknown unknowns" and "known unknowns" is that the estimates, called for by their model, are not required to meet any "quality control" tests.
Had they bothered to look into this issue more carefully, rather than make do with generalities, they would have realized that in the absence of "quality control" considerations, practically anything goes. After all, it is always possible to "estimate" the "unknowns". The question is: What interest would the "unknown unknowns" problem hold for us without some "quality control" requirements imposed -- either implicitly and/or explicitly -- on these "estimates"?
Ideed, in the absence of such controls, the quality of the results obtained are described by these two universally accepted maxims:
- Garbage in -- Garbage out (GIGO).
- Results are only as good as the estimates on which they are based.
And, if such maxims are of no concern, then an "unknown unknowns" problem is being trivialized to such a degree that it can practically be solved by assigning the parameters of interest any gross, crude, utterly questionable, non-sensical "estimates" that might strike our fancy.
The point is that if "quality" is not an issue, then it is always possible to come up with an estimate. Indeed, Click here to show/hide a simple recipe ...
A tested recipe for obtaining an estimate
Wet your index finger and put it in the air.
Think of a number and double it.See it online at http://wiki.answers.com/Q/What_is_best_estimate_and_how_do_i_calculate_it.
The role of these maxims is to remind us of the "quality" issue.
So, both conceptually and practically, the distinction between "unknown unknowns" and "known unknowns" comes down to the "quality" of the estimates that are associated with the "unknowns". Roughly:
- If the estimates meet our "quality control" requirements, then we are dealing with a "Known unknowns" problem.
- If the estimates do not meet our "quality control" requirements, then we are dealing with an "unknown uknowns" problem.
Of course, this does not mean that there are no gray areas between these two extreme. As a rule there are. But this fact is no excuse for blurring the distinction between them, especially in the context of specific mathematical models such as the one considered in the article under review.
In sum, the absence from this article of "quality control" requirements on the estimates of the problem's parameters essentially means that we are dealing here with a mathematical model for which "anything goes". This entails in turn that the distinction between "unknown unknown" and "known uknown" is non-existent.
Remark:
The last sentence of the article's abstract reads as follows:Our examination highlights the importance of being explicit about the objectives, costs and expected benefits of monitoring in a decision analytic framework.It is a pity that the authors' examination did not highlight the difficulties posed by the GIGO Axiom, and the importance of being explicit about the quality of the estimates used under severe uncertainty.
Conclusions
The article's concluding section makes the following statement (p. 12, emphasis is mine):
Increasing pressure on science and conservation budgets demands that investments in monitoring be as rigorously justified as possible. We support the argument that the design of a monitoring program should follow a rational, structured process that involves a clear articulation of the purpose of the program. We have provided a framework for such an examination of any monitoring program, and encourage those advocating surveillance monitoring to ground their justifications in the framework we have presented.It is important therefore to caution readers of this article that the framework presented in this article is grounded on a model involving "unknown unknown" parameters that end being treated as though they were "known unknowns". Surely this approach casts grave doubts on the framework as a whole. Indeed, it is hard to comprehend how anyone can justify a proposition to approach the solution of a problem involving "unknown unknowns" by simply positing that the "unknown unknowns" in question can be easily transformed into "known unknowns" through a "... blend of standard statistical approaches and expert-elicited estimation or bounding ...".
This position on "unknown unknowns" trivializes the idea to the extent of rendering it vacuous.
Finally, since the authors refer to the immensely popular concept Black Swan, it is apposite to point out that the lesson that the authors ought to have learned from Black Swans, aside from the definition of the "unpredictable", is the imperative to avoid an incautious treatment of the "unknown", the "unpredictable", etc. Taleb's merciless attacks on those who model the future on grounds of available knowledge (using standard statistical methods) should have prompted them to examine whether their approach to "unknown unknowns" might not indeed be incautious, in the very least too good to be true , hence certain to instill a false sense of security in the framework that they recommend.
It is indeed regrettable that such a mistreatment of Black Swans originated in the land of the Black Swan itself!
Even info-gap scholars appreciate this important point:
Interpreting these regions of "unknown unknowns" requires extreme caution because assessments made under severe lack of knowledge about invasion often display low risks and thus may promote a false confidence.
Denys Yemshanov, Frank H. Koch, Yakov Ben-Haim, and William D. Smith
Robustness of Risk Maps and Survey Networks to Knowledge Gaps About a New Invasive Pest
Risk Analysis, Vol. 30, No. 2, 261-276, 2010.And the moral of the story is this:
- A problem involving genuine "unknown unknowns" cannot be solved by mere rhetoric. No amount of rhetoric will transform "unknown unknowns" into "known unknowns".
- In the absence of "quality control" requirements on the parameters of the proposed model, the proposed methodology is shown by the universally accepted Garbage In -- Garbage Out maxim for what it is.
- If the thinking captured in the concepts "severe uncertainty", "knightian uncertainty", "Black Swans", "unknown unknowns", "known unknowns", etc., is to be represented in a formal mathematical model, it is imperative that this representation be consistent with the thinking conveyed by these ideas. Otherwise, these concepts are reduced to mere buzzwords .
- The title of the article is misleading. It should read: Allocating monitoring effort in the face of known unknowns.
This takes us back to info-gap decision theory.
By suggesting that true Knightian uncertainty can be properly treated by a (local) radius of stability model, info-gap decision theory completely dilutes the concept "Knightian uncertainty" and the difficulties that it poses to decision-makers.
Other Reviews
- Ben-Haim (2001, 2006): Info-Gap Decision Theory: decisions under severe uncertainty.
- Regan et al (2005): Robust decision-making under severe uncertainty for conservation management.
- Moilanen et al (2006): Planning for robust reserve networks using uncertainty analysis.
- Burgman (2008): Shakespeare, Wald and decision making under severe uncertainty.
- Ben-Haim and Demertzis (2008): Confidence in monetary policy.
- Hall and Harvey (2009): Decision making under severe uncertainty for flood risk management: a case study of info-gap robustness analysis.
- Ben-Haim (2009): Info-gap forecasting and the advantage of sub-optimal models.
- Yokomizo et al (2009): Managing the impact of invasive species: the value of knowing the density-impact curve.
- Davidovitch et al (2009): Info-gap theory and robust design of surveillance for invasive species: The case study of Barrow Island.
- Ben-Haim et al (2009): Do we know how to set decision thresholds for diabetes?
- Beresford and Thompson (2009): An info-gap approach to managing portfolios of assets with uncertain returns
- Ben-Haim, Dacso, Carrasco, and Rajan (2009): Heterogeneous uncertainties in cholesterol management
- Rout, Thompson, and McCarthy (2009): Robust decisions for declaring eradication of invasive species
- Ben-Haim (2010): Info-Gap Economics: An Operational Introduction
- Hine and Hall (2010): Information gap analysis of flood model uncertainties and regional frequency analysis
- Ben-Haim (2010): Interpreting Null Results from Measurements with Uncertain Correlations: An Info-Gap Approach
- Wintle et al. (2010): Allocating monitoring effort in the face of unknown unknowns
- Moffitt et al. (2010): Securing the Border from Invasives: Robust Inspections under Severe Uncertainty
- Yemshanov et al. (2010): Robustness of Risk Maps and Survey Networks to Knowledge Gaps About a New Invasive Pest
- Davidovitch and Ben-Haim (2010): Robust satisficing voting: why are uncertain voters biased towards sincerity?
- Schwartz et al. (2010): What Makes a Good Decision? Robust Satisficing as a Normative Standard of Rational Decision Making
- Arkadeb Ghosal et al. (2010): Computing Robustness of FlexRay Schedules to Uncertainties in Design Parameters
- Hemez et al. (2002): Info-gap robustness for the correlation of tests and simulations of a non-linear transient
- Hemez et al. (2003): Applying information-gap reasoning to the predictive accuracy assessment of transient dynamics simulations
- Hemez, F.M. and Ben-Haim, Y. (2004): Info-gap robustness for the correlation of tests and simulations of a non-linear transient
- Ben-Haim, Y. (2007): Frequently asked questions about info-gap decision theory
- Sprenger, J. (2011): The Precautionary Approach and the Role of Scientists in Environmental Decision-Making
- Sprenger, J. (2011): Precaution with the Precautionary Principle: How does it help in making decisions
- Hall et al. (2011): Robust climate policies under uncertainty: A comparison of Info--Gap and RDM methods
- Ben-Haim and Cogan (2011) : Linear bounds on an uncertain non-linear oscillator: an info-gap approach
- Van der Burg and Tyre (2011) : Integrating info-gap decision theory with robust population management: a case study using the Mountain Plover
- Hildebrandt and Knoke (2011) : Investment decisions under uncertainty --- A methodological review on forest science studies.
- Wintle et al. (2011) : Ecological-economic optimization of biodiversity conservation under climate change.
- Ranger et al. (2011) : Adaptation in the UK: a decision-making process.