The Spin Stops Here!
Decision-Making Under Severe Uncertainty  
Faqs | Help | @ | Contact | home  
voodoostan info-gap decision theory info-gap economics severe uncertainty mighty maximin robust decisions responsible decisions

Reviews of publications on Info-Gap decision theory

Review # 21 (Posted: October 10, 2010)

Reference:

Barry Schwartz, Yakov Ben-Haim, and Cliff Dacso
What Makes a Good Decision? Robust Satisficing as a Normative Standard of Rational Decision Making
The Journal for the Theory of Social Behaviour, in press, 2010.

Abstract Most decisions in life involve ambiguity, where probabilities can not be meaningfully specified, as much as they involve probabilistic uncertainty. In such conditions, the aspiration to utility maximization may be self-deceptive. We propose "robust satisficing" as an alternative to utility maximizing as the normative standard for rational decision making in such circumstances. Instead of seeking to maximize the expected value, or utility, of a decision outcome, robust satisficing aims to maximize the robustness to uncertainty of a satisfactory outcome. That is, robust satisficing asks, "what is a 'good enough' outcome," and then seeks the option that will produce such an outcome under the widest set of circumstances. We explore the conditions under which robust satisficing is a more appropriate norm for decision making than utility maximizing.
Scores TUIGF:100%
SNHNSNDN:3786%
GIGO:100%

Remark

This review is based on a pre-print of the article downloaded from

http://www.technion.ac.il/yakov/aaa-schwartz.doc

on September 26, 2010.

Once it is published, I shall revisit it to see whether this review requires any modification.

Overview

  Table of contents  
This is an extremely interesting article.

It's main interest lies of course in the proposition to substitute "utility maximization" with Info-gap's "robust satisficing". But, it is interesting for other reasons as well, foremost of which is its rhetoric. The authors have manage to raise info-gap's customary rhetoric -- which is quite significant in its own right -- to new and unprecedented heights, by bolstering it with an extra doze of rhetoric that is taken from the long-running but pointless indeed counter-productive debate on the topic of: satisficing vs optimizing .

The article's main proposition is then to use info-gap decision theory as the foundation for a new normative standard for decision making under severe uncertainty that is centered on info-gap decision theory's so called robust satisficing feature.

As I have already debunked info-gap decision theory, I could have dismissed the proposed new normative theory simply on the grounds that it is based on a  debunked theory.

I could have, but I shall not make do with this argument.

Because, it is important to bring to the readers' attention that in addition to the "old" errors and misconceptions that are already entrenched in the info-gap literature, this article puts forward new errors and misconceptions that must be addressed and debunked as well.

For example, this article puts forth what, to the best of my knowledge, is a new myth about info-gap decision theory, which asserts the following:

New Myth
Info-gap decision theory selects the decision that generates the widest range of satisfactory outcomes.

So, before we get started, it is important first of all to set the record straight on this claim:

Old Fact
Info-gap's robustness model is a model of local robustness. Therefore, by definition, it does not, much less is it able to, seek decisions with the widest range of satisfactory outcomes. All it can do is seek decisions that are robust against small perturbations in a given nominal value of the parameter of interest.

The immediate implication of this fact is of course that the authors are basing their purported new theory on a capability that info-gap decision theory by definition does not possess. This is sufficient grounds to dismiss the purported new theory out of hand.

However, for the sake of argument, suppose that the authors would counter as follows:

Granting that info-gap's robustness model does not select a decision with the widest range of satisfactory outcomes, as indeed required by the proposed new theory,

still, ...

this does not undermine the proposed new Robust Satisficing standard itself, because the standard can be backed up by some other model that does select a decision with the wideset range of satisfactory outcomes.

To which I say:

In this case, the proposed "new" Robust Satisficing standard is utterly redundant. Because, we already have at our disposal a methodology for robust decision making in the face of severe uncertainty proposing a model that does indeed do what info-gap's robustness model is incapable of doing. Namely, it selects a decision with the widest range of satisfactory outcomes. This methodology has been available at least since 1972!!!

The question is then: what is the point/merit of the proposed "new" standard, especially in view of it being based on a fundamentally flawed theory?

As you will see, it will take a relatively lengthy argument to make this obvious point clear ...

My intention is to come down hard on the info-gap foundation of the proposed "new" standard. But, I shall also have to address the "satisficing vs optimizing" facet of the proposed standard. This, however, I shall do very briefly, indeed reluctantly, because as my brief comments on this question will attest, I consider the continuing discussion on this question pointless.

So, given the rather lengthy commentary that follows this introduction, it is important that the readers have a clear picture of the authors' thesis, and the arguments that rebut them.

The Debunkee

The authors propose a normative standard that they call Robust Satisficing, to guide decision-making in the face of radical uncertainty. According to the authors,

  • The proposed Robust Satisficing approach to radical uncertainty is new.

  • It furnishes a standard for identifying decisions that maximize the range of satisfactory outcomes.

  • Minimax is a kind of cousin to the proposed Robust Satisficing approach.

The Debunker

To refute the purported new approach it is sufficient to show that

  • The proposed "Robust Satisficing" approach to radical uncertainty is not new. This type of approach goes back to at least the late 1960s, early 1970s.

  • The model that is at the center of the proposed approach, does not indeed cannot pursue decisions that maximize the range of satisfactory outcomes. All it can do is seek decisions that are robust in the neighborhood of a poor estimate of the true value of the parameter of interest.

  • The Maximin model is not a cousin of the proposed Robust Satisficing model. It is in fact its Grandmother (circa 1940) -- the Mother being the Radius of Stability model (circa 1960).

For the benefit of readers who are not at home with the topic of "decision-making under severe uncertainty", the list of facts that pulls the rug out from under the proposed approach is as follows:

  • The idea to regard the best decision (under conditions of severe uncertainty) as that which maximizes the range of satisfactory outcomes is not new, it had been proposed a long time ago (e.g. Rosenhead et al. 1972).

  • The proposed robustness model is a simple version of a model known universally as Radius of Stability (circa 1960).

  • The proposed robustness model is a simple instance of Wald's famous Maximin model (circa 1940).

  • The proposed robustness model is not designed to seek out decisions that maximizes the range of satisfactory outcomes.

  • The proposed robustness model is designed to handle small perturbations in a nominal value of the parameter of interest.

  • The proposed robustness model is therefore the wrong model for decision making in the face of radical uncertainty.

If you are familiar with my critique of info-gap decision theory you may perhaps assume that the ensuing review will be no more than a repetition of what I have been arguing all along ...

I therefore suggest that you continue reading because you are likely to learn more about info-gap decision theory's potential for leading astray ...

Still, for the benefit of readers who do not intend to read the remaining sections of the review, here is a summary of the main points of the discussion.

  • The proposition to use robust-satisficing as a "new" normative standard to guide sound decision-making in the face of radical uncertainty, in lieu of utility maximization which, the authors consider to be the prevailing approach in this area, suggest that the authors are unaware of the progress that has been made, over the past 40 years, in the study of "decision-making".

  • The authors' oblivion to the state of the art in this area is evidenced in the absence of all reference to the thriving area of Robust Optimization or to the area of Decisions with Multiple Objectives or to that of Multiple Criteria Decision-Making or to Pareto Optimization which, it is important to note, bears directly on their proposition.

  • This total oblivion to the state of the art puts the authors squarely on the path to reinventing the wheel, and a square one at that.

  • Because, as anyone even mildly conversant with robust decision-making under severe uncertainty can immediately see, the article's high aspirations to provide no less than a new "normative standard for rational decision making" under conditions of "radical uncertainty", in fact take us back to models of the early 1970s, namely to models predating new developments in the areas of robust decision-making and multiple objective decision-making.

  • The authors' approach to dealing with radical uncertainty is essentially in line with info-gap decision theory's prescription for managing radical uncertainty, which -- as I have been arguing -- is in contravention of the Garbage In -- Garbage Out (GIGO) and similar maxims, and which therefore places it squarely in the voodoo theories camp.

  • The authors thus continue to perpetuate the myth (entrenched in the info-gap literature) that info-gap's robustness model is particularly suitable for handling situations subject to severe (radical) uncertainty where the uncertainty space is vast, the estimate is poor, and the uncertainty model is likelihood-free.

  • The authors also continue to misrepresent the facts about the true relation between info-gap's robustness model and the Maximin model.

These statements are explained and corroborated in the Appendix. For a quick check, simply go to the short mobile debunker of info-gap decision theory.

Appendix

Search/Selection Committee

Reading the article under review, the question that immediately springs to mind is this:

Let us assume that it is indeed a good idea to challenge the hegemony of what the authors claim is the prevailing approach to dealing with severe uncertainty, namely "utility maximization", and to replace it with a new "maximize the robustness of a given satisfaction level" approach.

I hasten to add that I am neither for or against, or whatever. I merely assume, for the purposes of this discussion, that this proposition is on the agenda.

In this case, assume next that we establish a Search/Selection Committee to find the most suitable robust satisficing theory to do the job.

Because, why settle for less?

To do this, the Committee would surely have to read the literature on robust decision-making in the face of radical uncertainty so as to be in a position to select the most appropriate robustness theory for dealing with radical uncertainty.

It would also have to read the literature on multiple objective decision-making so as to be able to select the most appropriate theory capable of dealing with a problem of two conflicting objectives: robustness vs satisfaction level.

Because, why settle for less?

In particular, why should it adopt a debunked theory for this purpose?!?!

Clearly, what I am driving at is that as the article under review was published in a peer-reviewed journal, it must be treated as a scholarly work. So, the main issues that it should have addressed are these:

This is what one would have expected from a scholarly analysis of the authors' basic proposition, and this is what the paper's referees should have demanded that the authors do.

But this is not what the article does.

What is particularly striking about the article is its total disregard of the state of the art in robust decision-making, as evidenced in its grossly misleading, uncritical, assessment of info-gap decision theory as the "selected" method.

So, obviously, my review will have to deal with a host of methodological and technical issues. I plan to do this in stages, and I expect that the complete review will be ready by the end of the year (2010).

Stay tuned ...!

Where is Robustness Optimization?

The main tenor of this article article is that info-gap decision theory is the only available theory of robust decision-making in the face of uncertainty. I discuss this issue in detail in the section entitled State of the art.

At this preliminary stage, I just want to point out that robust decision-making in the face of severe uncertainty is a well-established area of research and application. Particularly relevant to this article is the the thriving field of Robust Optimization which is concerned with precisely the type of robustness issues that are discussed in the article.

Yet, not one single reference is made in the article to this fact!

As I explain in the section State of the art, this is not an isolated case. The info-gap literature systematically, and one suspects deliberately, avoids any mention of the area of Robust Optimization.

So:

For the benefit of readers who are not at home with the topic of optimization, notably with that of Robust optimization, it is important to point out the following.

The authors' proposition to substitute "utility maximization" with "robust satisficing" not only takes no account of developments in the field of Robust Optimization that bear directly on this proposition. It is based in fact on a profound misrepresentation of the whole concept of optimization, hence of what an optimization problem is all about. Because the othors’ underlying proposition is based on the gospel of "satisficing is better than optimizing", their basic position is then the following. "Optimization" only seeks to maximize an objective -- which is not really all that good -- whereas, satisficing makes do with less than maximizing ... but in the end accomplishes more: the satisfaction of a specified outcome which is a much better thing.

Note then that an optimization problem poses two tasks:

For example, you may want to find the most reliable electronic device for a given job subject to budgetary and operational constraints. Or you may wish to find the most robust system that satisfices certain performance requirements.

The bottom line is that satisficing is an integral part of "optimizing" and therefore "robust-satisficing" is a special case of "robust optimizing".

Needless to say, the treatment of severe uncertainty is an issue of prime importance in Robust Optimization, because, in this context, robustness is sought against uncertainty in the true value of a parameter of the problem under consideration.

All this can be summed up as follows: a robust solution to an optimization problem is a solution that performs well (according to pre-determined performance criteria) with respect to the objective function and/or the constraints of the problem over a range of values of the parameter of interest.

Now back to the article under review.

The robustness considered in the article is described as follows (page 1):

That is, robust satisficing asks, "what is a 'good enough' outcome," and then seeks the option that will produce such an outcome under the widest set of circumstances.

The radical uncertainty is manifested in the lack of knowledge as to which "circumstance" will be realized. Namely, there is a radical uncertainty regarding which element of the set of possible circumstances will be realized. We thus seek an option (decision) that is most robust against this radical uncertainty.

That said, I hasten to point out that the fundamental flaws in info-gap decision theory render it utterly unsuitable for this task. More on this can be found in the mobile debunker of info-gap decision theory and in subsequent sections of this review.

My objective is then to explain how grossly misleading the above quoted description of "robust satisficing" is, given that it is based on info-gap decision theory. That is, to explain that the proposed new normative theory does not (cannot) even handle (conceptually) trivially simple tasks.

How do we determine what is 'good enough'?

The first point that must be made abundantly clear is that when the authors say that "robust satisficing asks, 'what is a 'good enough' outcome?", the term "asks" does not designate a method, a procedure, guidelines, or what have you, instructing or enlightening us on how to determine what is 'good enough'. Indeed, the proposed theory does not even begin to "ask" this rudimentary question, it simply posits that we begin with a fully fledged predetermined 'good enough' outcome" in hand.

But the whole point is that this is precisely where our difficulties lie. Generally, in problems depicting situations of conflicts between objectives -- the "good enough outcome" and other objectives -- an answer to the question "What is a good enough outcome?" is hardly straightforward. In other words, in general, to determine what is a 'good enough outcome' we need to know how changes in the value of the 'good enough outcome' affect the values of other objectives.

And in the case under consideration, we cannot decide what is a 'good enough outcome' without knowing the value of the associated robustness against radical uncertainty, because the higher the value of the 'good enough outcome', the lower its robustness against radical uncertainty.

So, how are we going to decide what is the appropriate balance or tradeoff between the 'good enough outcome' and robustness to radical uncertainty?

The proposed new theory does not even bother to address this fundamental issue.

Its underlying assumption is that the value of the 'good enough outcome' is given and all that is left to do is to determine the robustness of this given value of the 'good enough outcome' to radical uncertainty.

Where is the estimate?

As the proposed "robust satisficing" normative standard is anchored in info-gap decision theory, it is important to be clear on the following point:

The centerpiece of info-gap decision theory is a robustness model and the fulcrum of this robustness model is an estimate of the true value of the parameter of interest. It is the true value of this parameter that is subject to radical uncertainty. This means that info-gap's robustness analysis revolves around this estimate. There is no info-gap analysis without an estimate being at the center of this analysis.

And yet, this important fact is not only not discussed in the article, it is absent from the authors' description of info-gap's robustness analysis that "... seeks the option ... " namely the (purportedly) acceptably satisfactory decision.

So to give you an idea of how the (info-gap) robustness model underlying the "robust satisficing" analysis proposed in this article should have been explained, consider the following:

Let:

Note that, given the radical uncertainty, all we know about the true value of u is that it is an element of U. We shall refer to the set U as the uncertainty space of the problem.

Next, let:

Formally, S(d) is a subset of U which contains the values of u in U that are satisfactory with respect to decision d.

Hence:

The definition of robustness according to info-gap decision theory:
The robustness of decision d is the size of the largest neighborhood around the estimate û, all of whose elements are satisfactory with respect to decision d.

In other words, the robustness of decision d is the size of the largest neighborhood around the estimate û, that is a subset of S(d).

It is important to note that the "neighborhoods" around the estimate that designate the robustness of decisions are required by the axioms of info-gap decision theory to to be nested. Think about them as "balls" centered at the estimate, so that the size of a neighborhood would be equal to the radius of the ball representing the neighborhood.

This means of course that the robustness of decision d can be stated as follows:

The robustness of decision d is the radius of the largest ball around the estimate û that is contained in S(d).

Obviously, this concept is known universally as Radius of stability (circa 1960). But, info-gap scholars are apparently unaware of this fact, insisting as they do that this is a new concept that is radically different from other measures of robustness.

Clearly then, to formulate an info-gap definition of robustness we need an estimate of the true value of u. Without an estimate of the true value of u there is no info-gap robustness analysis. in other words, without stipulating an estimate we cannot use info-gap decision theory.

But, this 'trifle" is not even mentioned in the article.

The following example is designed then to illustrate the utter absurd that the robustness model proposed in this article gives rise to in the absence of an estimate of the true value of u. In other words, the idea is to illustrate that, without an estimate, it impossible to use the proposed "new" normative standard even in situations where the problem is trivial.

Example

Consider the following picture where the large rectangle represents the uncertainty space U and the shaded area represents the set S(d) for some decision d.

Since S(d) covers most of U, it follows that most of the values of u in U are "satisfactory" and therefore we would have no doubts to deem decision d robust against the radical uncertainty in the true value of u. No formal analysis is required to reach this obvious conclusion.

However, as things stand, the robustness of decision d cannot be assessed/determined according to the precepts of info-gap decision theory because, as the picture illustrates, there is no point in U to represent an estimate of the true value of u.

Clearly, the radius of the largest ball contained in the shaded area would depend on the location of the center of the ball (estimate û). In other words, the value of the estimate û plays a central role in determining the robustness of decisions in info-gap decision theory.

To reiterate, given that the robustness of decision d, according to info-gap decision theory, hangs on the location of the estimate û in U, in the absence of the estimate we cannot determine the robustness of d.

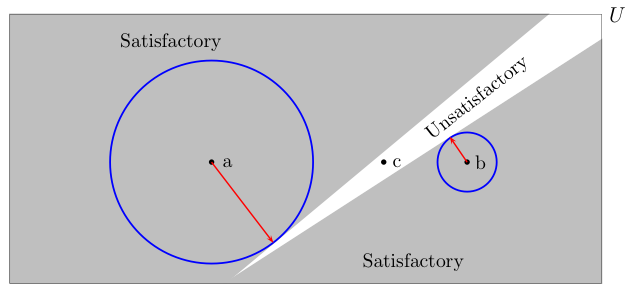
This feature of info-gap's robustness model is illustrated in the next picture, where the robustness of decision d is determined for three different values of the estimate û, denoted by a, b and c.

In short, it is patently clear that according to the precepts of info-gap decision theory, the robustness of decisions is crucially sensitive to the "location" of the estimate û in the uncertainty space U.

Some readers may wonder why I go into such lengths to elaborate this obvious point. So let me explain.

What I wanted to make clear through this analysis is not only that the authors' depiction of the robustness analysis, which underlies the proposed "robust satisficing" standard, is (according to Info-gap decision theory) utterly misleading. Indeed, this analysis enables me to bring out the fundamental flaw of info-gap decision theory itself.

One of the basic characteristics of radical uncertainty is that the estimates (of parameters) are poor, so much so that they can be substantially wrong. This fact is acknowledged in the info-gap literature, where the estimate û is often called a guess.

Another important point to keep in mind is that models of radical uncertainty are likelihood-free. That is, there is no ground to assume that the true value of u is more/less likely to be in any one particular neighborhood of the uncertainty space U. Specifically, there is no ground to assume that the true value of u is more likely to be in the neighborhood of the estimate û rather than in the neighborhood of any other point in U.

The implication is therefore clear. If we want to determine the robustness of a decision against radical uncertainty in the true value of u, there is no ground whatsoever to single out, for the robustness analysis, the neighborhood of the estimate û, or for that matter the neighborhood of any other given point in U. Hence, there is clearly no justification whatsoever to conduct the robustness analysis only on the neighborhood of the estimate û, or for that matter only on the neighborhood of any other given point in U.

But this is precisely what info-gap decision theory does, and this is precisely what earns this theory the title voodoo decision theory.

The point is that the treatment of radical uncertainty requires models of global robustness whereas info-gap decision theory treats radical uncertainty by means of a model of local robustness.

Fooled by robustness

Although the term "robustness" clearly has a familiar ring to it, it may have different meanings in different contexts. Hence, it is of the utmost importance to be clear on the definition of robustness that one uses in a specific context.

The authors do not provide a formal definition of the robustness that they have in mind, but they do explain what they mean by "robust satisficing" in the context of various examples.

Alas, these descriptions are inconsistent

For example, compare these three cases:

CasePageDescription in the article
A

1 That is, robust satisficing asks, "what is a 'good enough' outcome," and then seeks the option that will produce such an outcome under the widest set of circumstances.
B9-10 The robust satisficer answers two questions: first, what will be a "good enough" or satisfactory outcome; and second, of the options that will produce a good enough outcome, which one will do so under the widest range of possible future states of the world.
C19 A robust satisficing decision (perhaps about pollution abatement) is one whose outcome is acceptable for the widest range of possible errors in the best estimate.

Note that in Case C there is a reference to something called best estimate which is conspicuously missing from Case A and Case B. Moreover, the authors do not state what this best estimate is. In other words, an estimate of what is it?

In fact, as indicated in the preceding section, the authors keep mum on the essential fact that an estimate of the unknown true value of the parameter of interest is the center of info-gap's robust-satisficing model; the true value of this parameter being subject to radical uncertainty.

Hence, the descriptions of Case A and Case B are misleading because they are incompatible with the (info-gap) robustness model that underlies the proposed theory. This means of course -- as indicated in the preceding section -- that the proposed new normative theory for decision-making under radical uncertainty cannot handle even a simple problem such this.

Example

Consider a case with two decisions, d' and d'' where the uncertainty space U is a rectangle, as shown below. First, suppose that there is no estimate for the true value of u.

Decision d'

In the picture, the large rectangle U represents the uncertainty space associated with the problem. This is the set of all the possible values of the parameter of interest whose true value is subject to radical uncertainty. The shaded area represents values of this parameter for which decision d' satisfies the performance requirement.

Since most of the area of U is shaded, decision d' is decidedly robust against the radical uncertainty in the true value of the parameter of interest.

Decision d''

In the picture, the large rectangle U represents the uncertainty space associated with the problem. This is the set of all the possible values of the parameter of interest whose true value is subject to radical uncertainty. The shaded area represents values of the parameter for which decision d'' satisfies the performance requirement.

Since most of the area of U is not shaded, decision d'' cannot be deemed robust against the radical uncertainty in the true value of the parameter of interest.

Question: Which of the two decisions (d', d'') is more robust against the radical uncertainty in the true value of the parameter of interest?
Answer: Sorry, Mate!
Info-gap decision theory cannot answer this simple question. To answer this question info-gap decision theory requires an estimate of the true value of u.

Suppose then that in view of this situation you turn to a consulting company, Estimates Galore, instructing them to work out an estimate of the true value of u. So, $100,000 later you receive a report from Estimates Galore offering 6 different estimates, call them û(1), û(1), ..., û(6), obtained from 6 different established scientific methods.

Equipped with these 6 estimates, you now ask the local info-gap expert to determine which decision, d' or d'' is the more robust, given these 6 estimates.

However, to your great surprise, you will be advised by the local info-gap expert that info-gap decision theory cannot handle 6 estimates. More precisely, the theory requires exactly one estimate. And so ... you will go right back to where you started ...

In other words, it is important to appreciate that because the new normative theory, proposed in the article, is rooted in info-gap decision theory, it necessarily suffers from all the ills afflicting info-gap decision theory. So, although the authors keep mum on the centrality of the estimate, note that info-gap's robustness model conducts the robustness analysis in the neighborhood of a point estimate of the true value of the parameter of interest. Thus, the robustness of decision d is the size of the largest neighborhood around the point estimate all of whose elements are satisfactory with respect to decision d.

To examine then how the proposed new theory would address the above case, let us modify it a bit and assume that, for a bargain of $20,000 extra, Estimates Galore provided you with a single point estimate, û, of the true value of the parameter of interest. In the pictures below, this estimate is represented by a black dot • in the rectangle representing the uncertainty space U associated with the problem.

Decision d'

The large rectangle U represents in the pictures the uncertainty space associated with the problem, and the point estimate is represented by the dark black dot.

The largest neighborhood around the estimate, all of whose elements satisfy the performance constraint imposed on decision d', is represented by the blue circle. The length of the radius of this circle is the robustness of decision d'.

Decision d''

The large rectangle U represents in picture the uncertainty space associated with the problem, and the point estimate is represented by the dark black dot.

The largest neighborhood around the estimate whose elements satisfy the performance constraint imposed on decision d'' is represented by the blue circle. The length of the radius of this circle is the robustness of decision d''.

Question: Which of the two decisions (d', d'') is more robust against the radical uncertainty in the true value of the parameter of interest?
Answer: According to the proposed new theory, decision d'' is much more robust than d' against the radical uncertainty in the true value of the parameter of interest.
The bottom line:
The proposed new normative theory does not (cannot) seek decisions that are most robust against the radical uncertainty in the true value of the parameter of interest.

It can only seek decisions that are most robust against small perturbations in the value of the point estimate of the true value of the parameter of interest.

The following simple example illustrates how absurd the proposed new theory is.

Example

To see why the proposed theory is utterly unsuitable for the treatment of radical uncertainty, consider the case where the uncertainty space is the real line, namely the true value of the parameter can be any real number, so U = (−∞,∞).

Now suppose that there are two decisions (options), say d' and d'', and that the estimate of the true value of u is equal to 0. Also, assume that the ranges of satisfactory values of the parameter u is the interval I' = [-1,1] for decision d' and the union of the intervals (−∞,-1], [-0.9,0.9] and [1,∞] for d'', namely let I''= (−∞,-1] ∪ [-0.9,0.9] ∪ [1,∞).

According to the proposed new theory, the winner is ... decision d'.

To appreciate the absurd in this verdict, consider the picture depicting the situation:

In this case the simple facts are as follows:

No amount of rhetoric can explain away the absurd of this evaluation.

Local vs Global robustness

It is important to keep in mind that conditions of radical uncertainty mean that the estimate is poor and the uncertainty model is likelihood-free. This means that there are no grounds to assume that the true value of the parameter is in the neighborhood of the estimate, hence the robustness that must be sought must be global rather than local. The implication therefore is that info-gap's robustness model is the wrong tool for the job. By definition, info-gap's robustness model seeks decisions that are robust in the locale of a given poor estimate. But, to deal properly with radical uncertainty, a robustness model must be able to seek decisions that are robust globally, namely in relation to the entire uncertainty space under consideration.

The authors apparently are unaware of the distinction between local and global robustness, because they erroneously treat info-gap's robustness model as a model of global robustness. This explains their strong (but grossly erroneous) conviction that info-gap's robustness model generates decisions whose performance is satisfactory under the widest range of circumstances.

As shown in the preceding examples, there is no assurance that the proposed new theory will select a decision whose performance is satisfactory under the widest range of circumstances. It therefore cannot be counted on to select a decision whose performance is satisfactory under the widest range of circumstances.

For instance, consider again the following case:

Clearly, the widest range of satisfactory outcomes is provided by the decision associated with I''. But, according to the proposed new theory, the most robust decision is the one associated with I'.

Yet, the authors repeatedly claim that this is so (emphasis is mine):

On Page 1 we read:
That is, robust satisficing asks, "what is a ‘good enough’ outcome," and then seeks the option that will produce such an outcome under the widest set of circumstances.
On page Page 9-10 we read :
The robust satisficer answers two questions: first, what will be a “good enough” or satisfactory outcome; and second, of the options that will produce a good enough outcome, which one will do so under the widest range of possible future states of the world.
On page 19 we read:
A robust satisficing decision (perhaps about pollution abatement) is one whose outcome is acceptable for the widest range of possible errors in the best estimate. No probability is presumed or employed.
On page 21 we read:
4. I want $1 million when I retire. What investment strategy will get me that million under the widest range of conditions?
On page 21 we read:
But an investment strategy that aims to get you a million dollars under the widest set of circumstances is likely to be very different from one that aims to maximize the current estimate of future return on investment.
On page 22 we read:
A business operating with an eye toward robust satisficing asks not, “How can we maximize return on investment in the coming year?” It asks, instead, “What kind of return do we want in the coming year, say, in order to compare favorably with the competition? And what strategy will get us that return under the widest array of circumstances?”
On page 27 we read:
For an individual who recognizes the costliness of decision making, and who identifies adequate (as opposed to extreme) gains that must be attained, a satisficing approach will achieve those gains for the widest range of contingencies.

These claims are without any foundation, they are in fact false hence, grossly misleading.

The proposed robustness model seeks decisions that maximize the size of the set of satisfactory outcomes in the neighborhood around a poor estimate of the parameter of interest, not the widest set of satisfactory outcomes.

Now, on page 25 the authors argue that:

But there are also strategic situations in which robust satisficing makes sense (see Ben-Haim & Hippel, 2002 for a discussion of the Cuban missile crisis; and Davidovitch & Ben-Haim, in press, for a discussion of the strategic decisions of voters).

There are of course situations where the ranking of decisions based on local robustness is equivalent to that of global robustness. For example, consider the opening paragraph of the article entitled Global stability of population models by Cull (1981, p. 47, Bulletin of Mathematical Biology, Vol. 43, pp. 47-58.):

It is well known that local and global stability are not equivalent and that it is much easier to test for local stability than for global stability (see LaSalle, 1976). The point of this paper is to show that for the usual one-dimensional population models, local and global stability are equivalent.

However, it is eminently clear that info-gap decision theory does not, indeed cannot -- methodologically speaking -- provide any evidence or proof in support of its generic robustness model’s capability to produce such results. Therefore, the duty to find a way out of this impasse is left to the users of this theory, who must do this on a case-by-case basis. Thus, it is not surprising that, once made aware of this situation, some info-gap scholars have attempted to provide some sort of evidence, or proof, or logic, to justify their use of info-gap's robustness model.

I discuss this in a subsection section entitled Fixing the square wheel.

From a robust optimization perspective, models of local robustness are regarded as unsuitable for the treatment of severe uncertainty, especially in cases where the uncertainty space is large. For example, Ben-Tal et al. (2009, European Journal of Operational Research, 199(3), 922-935) view models that restrict the robustness analysis only to the range of "normal" values of the parameter as representing a "somewhat 'irresponsible' decision maker".

I go one step further and argue that the use of a Radius of Stability model for the treatment of radical uncertainty associated with unbounded regions of uncertainty amounts to ... voodoo decision-making.

To sum it all up, the authors' claims that the proposed theory seeks decisions that provide the widest range of circumstances where the decisions performs satisfactorily are groundless. These claims are therefore grossly misleading.

It would appear that the authors were taken in by their own rhetoric ...

Reinventing a square wheel

The proposed theory is a reinvented square wheel for the same reasons that info-gap decision theory is a reinvented square wheel.

To explain.

Info-gap decision theory is claimed to be a new theory that is radically different from all current theories of decision under uncertainty. The truth of course is that info-gap's robustness model is a simple Radius of Stability model (circa 1960). Furthermore, info-gap's robustness model is also a simple instance of Wald's famous Maximin model (circa 1940), by far the most prevalent and well-known model for robust decision-making under severe uncertainty. These facts earn it the title "a reinvented wheel".

As for being a "reinvented square wheel".

Info-gap's misapplication of its robustness model, namely its prescription to use its robustness model -- which, as we saw, yields local rather than global robustness -- in the management of severe uncertainty, renders it a reinvented square wheel.

Fixing the square wheel

A number of (unsuccessful) attempts have been made recently by a number of info-gap scholars, presumably in view of my criticism of info-gap decision theory, to correct this fundamental flaw in info-gap's uncertainty model.

For instance, in Hall and Harvey (2009, p. 2) we read:
An assumption remains that values of u become increasingly unlikely as they diverge from û.
and in Hine and Hall (2010, p. 203) we read:
The main assumption is that u, albeit uncertain, will to some extent be clustered around some central estimate û in the way described by U(α,û), though the size of the cluster (the horizon of uncertainty α) is unknown. In other words, there is no known or meaningfully bounded worst case. Specification of the info gap uncertainty model U(α,û) may be based upon current observations or best future projections.

A more difficult to identify "quick fix" is hidden in Rout et al. (2009, p. 785):

Thus, the method challenges us to question our belief in the nominal estimate, so that we evaluate whether differences within the horizon of uncertainty are 'plausible'. Our uncertainty should not be so severe that a reasonable nominal estimate cannot be selected.

Apparently, contrary to the above, the authors of the article under review continue to hold that a local robustness analysis in the neighborhood of a poor estimate is a reliable method for the treatment of radical uncertainty.

If this is indeed the case, than the authors need reminding that the basic difficulty in decision-making under radical uncertainty is precisely the fact that such an analysis is unreliable because in this environment the estimate is poor and unreliable. And just in case, ... they should also be reminded that results can be only as good as the estimates on which they are based.

They should also be advised that this is the reason that the Radius of Stability model is used only in the analysis of small perturbations in a nominal value of a parameter. Hence, it cannot be used to determine the robustness of decisions against radical uncertainty.

Where is Pareto Optimization?

The decision problem considered in the article is a typical Pareto Optimization problem: negotiating between conflicting objectives. Thus, in the case of the problem studied in the article, the task is to achieve the largest robustness possible and at the same time achieve the highest possible required satisfaction level.

This concept is used extensively in multiobjective optimization.

So from this perspective, the model under consideration is a typical multiobjective optimization model.

What is particularly objectionable about the authors' depiction of this problem is that they discuss tradeoffs between robustness and satisfaction levels, referring to a (probabilistic) multi-attribute utility analysis , but they keep mum on, what is far more pertinent to and bears directly on the problem they consider, namely Multiobjective Optimization in general, and Pareto Optimization in particular.

Go figure!

The Maximin saga ...

On page 25 the authors claim the following:
Various suggestions have been proposed for making decisions in competitive strategic games. A common one is what is called the "minimax" strategy: choose the option with which you do as well as you can if the worst happens. Though you can't specify how likely it is that the worst will happen, adopting this strategy is a kind of insurance policy against total disaster. Minimax is a kind of cousin to robust satisficing, but it is not the same. First, at least sometimes, you can't even specify what the worst possible outcome can bring. In such situations, a minimax strategy is unhelpful. Second, and more important, robust satisficing is a way to manage uncertainty, not a way to manage bad outcomes. In choosing Brown over Swarthmore, you are not insuring a tolerable outcome if the worst happens. You are acting to produce a good-enough outcome if any of a large number of things happen. There are certainly situations in which minimax strategies make sense.

Before I turn to a detailed examination of specific claims in this paragraph about the so called "minimax" strategy and its relation to the so called "robust satisficing" strategy (read info-gap's robustness model), it is important to call attention to the following three facts.

Fact 1:
Not a single reference is given here to the "minimax" literature to enable the readers to see for themselves whether the authors' claims about "minimax" are sound, nor to support the various claims in this paragraph regarding the relationship between the "minimax" strategy and info-gap's robustness model.

Fact 2:
There are formal, rigorous proofs that info-gap's robustness model is a very simple instance (special case) of Wald's Maximin model (circa 1940). Thus, the authors' comments on what they call a "minimax" strategy are factually wrong and misleading. The bottom line is that whenever info-gap's robustness model is capable of handling the (local) "worst case" pertaining to "robust satisficing", so can its Maximin counterpart.

Fact 3:
The second author -- The Father of info-gap decision theory -- is aware of the fact that such theorems and proofs exist.

That said, let us examine some of the specific claims in this paragraph, starting with this:

A common one is what is called the "minimax" strategy: choose the option with which you do as well as you can if the worst happens.

But this is an inaccurate description of the "minimax" strategy. The point is that each option may have its own worst case. Here is Rawls' (1971, p. 152) famous description of the (methodologically equivalent) Maximin strategy

The maximin rule tells us to rank alternatives by their worst possible outcomes: we are to adopt the alternative the worst outcome of which is superior to the worst outcome of the others.

So, each decision may have its own worst outcome which means that it is erroneous to talk about a (general) worst outcome.

Next, consider this pearl:

Minimax is a kind of cousin to robust satisficing, but it is not the same.

This claim is doubly misleading because it gives the false impression that the robust-satisficing model proposed by the authors, that is info-gap's robustness model, and Wald's Maximin model, are on a par, but "not the same". Note then that the basic facts about the relation between these two models are as follows:

For formal proofs see the Mobile Debunker of Info-Gap Decision Theory.

Next, consider this claim:

First, at least sometimes, you can't even specify what the worst possible outcome can bring. In such situations, a minimax strategy is unhelpful.

This claim is grossly misleading because it implies that info-gap's robustness model has an advantage on the Maximin model in that its application does not require that a worst outcome exist. The relevant facts are as follows:

In other words, the above comparison between the (generic) Maximin model and info-gap's robustness model is wrong because it compares a supposed implementation of the prototype with an implementation of an instance of the prototype. But, a valid comparison can be made only between instances of the prototype. The inference is then that in cases where existence/knowledge of the worst case is not an issue for info-gap's robustness model, then this is also not an issue for that particular instance of the Maximin model that represents info-gap's robustness model.

Regarding the Family tree of info-gap decision theory, the relevant facts are as follows:

The basic dates are these:

These facts are there for all to see, and no amount of (misleading) rhetoric can explain them away.

In fact, a number of info-gap scholars have already conceded that info-gap's robustness model is a Maximin model (for example, see Review of Beresford-Smith and Thompson (2009) article.).

And finally consider the following cryptic statement:

Second, and more important, robust satisficing is a way to manage uncertainty, not a way to manage bad outcomes.

Are the authors suggesting that Wald's Maximin model is not "a way to manage" uncertainty? If so, then the authors would do well to read introductory books on decision theory. They will discover that Wald's maximin model is the foremost model offered by classical decision theory for the management of radical uncertainty.

For example, in French (1988) the maximin model is discussed in Chapter 2: Decisions under strict uncertainty, and where the question addressed is as follows (page 36): "How should a decision maker choose a in a situation of strict uncertainty?"

In Resnik (1987) the model is introduced in Chapter 2: Decisions under ignorance, where on page 26, the statement introducing the Maximin model is the following: " ... using ordinal utility functions we can formulate a very simple rule for making decisions under ignorance. "

In Ragsdale (2004):, it appears in Chapter 15: Decision Analysis, where in section 15.6: Nonprobabiisitc methods, we read (page 760):

The decision rules we will discuss can be divided into two categories: those that assume that probabilities of occurrence can be assigned to the states of nature in a decision problem (probabilistic methods), and those that do not (nonprobabilisitc methods).

And how about the entry Robust Control by Noah Williams (Dictionary of Economics, 2008; emphasis is mine):

Robust control is an approach for confronting model uncertainty in decision making, aiming at finding decision rules which perform well across a range of alternative models. This typically leads to a minimax approach, where the robust decision rule minimizes the worst-case outcome from the possible set. This article discusses the rationale for robust decisions, the background literature in control theory, and different approaches which have been used in economics, including the most prominent approach due to Hansen and Sargent.

The suggestion that Wald's Maximin model is not used in decision theory to model uncertainty is ludicrous.

I should also point out that according to the two primary text on info-gap decision theory (Ben-Haim 2001, 2006), info-gap robsut-satisficing is not just about managing uncertainty. Rather it is about the pursuit of decisions that are robust against severe uncertainty. Recall, however, that as indicated above, info-gap's robustness model is utterly unsuitable for this task.

And the irony is ....

All the authors have to do to achieve the robustness that they seem to be interested in, namely the widest range of satisfactory outcomes, is to use the following simple Maximin model (expressed in the MP format):

robust(d):= max {size(Y): Y⊆U, u∈S(d),∀u∈Y}

where size(Y) denotes the size of set Y, namely the range of values of u contained in Y. If Y is a finite set then size(Y) could be the cardinality of Y.

And if you insist on using the classic Maximin format, here it is:

max min   f(Y,u,d)
  Y⊆U   u∈Y
where

f(Y,u,d):= size(Y) , if u∈S(d)

and

f(Y,u,d):= 0 , if u∉S(d)

For the record, robustness models based on "widest range of satisfactory outcomes" date back to Starr (1963, 1966), Rosenhead et al. (1972), Rosenblat (1987), and many others. The reason that they are not used widely in practice is that it is often extremely difficult to solve the optimization problem induced by these models.

Robust satisficing vs utility maximizing

The rhetoric in this article about the supposed superiority of satisficing over optimizing is counter productive and amounts to no more than word games.

Consider, for instance what Jan Odhnoff said about this matter a long time ago:

In my opinion there is room for both 'optimizing' and 'satisficing' models in business economics. Unfortunately, the difference between 'optimizing' and 'satisficing' is often referred to as a difference in the quality of a certain choice. It is a triviality that an optimal result in an optimization can be an unsatisfactory result in a satisficing model. The best things would therefore be to avoid a general use of these two words.

Odhnoff, Jan, (1965).
On the Techniques of Optimizing and Satisficing.
The Swedish Journal of Economics, 67(1), 24-39.

But what is more:

It is elementary to show that any satisficing problem can be easily transformed into an equivalent optimization problem. Hence, the distinction between "satisficing" and "optimizing" is a mater of style, not of substance. What is important is to determine what to optimize and what to satisfice.

For the same reason, the distinction between robust-satisficing and utility maximization is spurious. Because, if in the case you are concerned with you define utility as "robustness" and maximize this utility, then in effect you are maximizing robustness, which is precisely what robust-satisficing does.

It is therefore interesting to note that in the 2001 version of the info-gap book (Ben-Haim (2001)), the term robust-optimizing is used to describe what the theory does. This term was changed to robust-satisficing in the 2006 edition of the book.

But, word games cannot salvage the serious flaws in info-gap decision theory. The flaws are foundational and no amount of rhetoric can fix them.

Example

To illustrate the above points, consider one of the examples mentioned in the paper (p. 21):

4. I want $1 million when I retire. What investment strategy will get me that million under the widest range of conditions?

First, to be able to appreciate why this problem is treated (by the authors) as a satisficing problem, let us ignore the specific robustness requirement "under the widest range of conditions", and let us concentrate on the problem’s main task.

Then, expressing this task in terms of a "saisficing problem", yields the following problem formulation:

Satisficing Problem:
Find an investment strategy x∈X such that r(x)≤$1000,000, where X denotes the set of available investment strategies and r(x) denotes the return ($) from investment x. Let X* denotes the set of all the investment strategies that satisfy this requirement.

Convince yourself that the following optimization problem is equivalent to this "satisficing problem":

Optimizing Problem:       max {f(x): x∈X}

where f is a real-valued function on X such that f(x)=r(x) if r(x)≥1000,000 and f(x)=1000,000 if r(x)>1000,000. Let Xo denote the set of (optimal) solutions to this problem.

Then clearly, X*=Xo.

Now, let us go back to the robust satisficing problem under consideration, namely

4. I want $1 million when I retire. What investment strategy will get me that million under the widest range of conditions?

Let u denote the uncertain parameter, U denote the parameter space, and r(x,u) denote the return from investment strategy x given u. So the "condition" is r(x,u)≥1,000,000.

Therefore, the robustness problem under consideration is as follows:

Robust satisficing problem:

Find an x in X such that the set {u∈U: r(x,u)≥1,000,000} is as large as possible.

Convince yourself that this problem is equivalent to the following optimization problem:

Robust optimization problem:

max {ρ(Y): r(x,u)≥1,000,000, ∀u∈Y}
x∈X,Y⊆U

where ρ(Y) denotes the size of set Y.

So what is so special about "robust satisficing" that cannot be (achieved) by "robust optimizing"?

Info-gap enthusiasts take note: the above formulation of the robust optimization problem is a Maximin model (MP format), but it is not an info-gap's robustnenss model!!!!!

Exercise: Transform the above Maximin formulation of the robust optimization problem from the MP format to the Classic format.

Hint: Have a look at And the irony is ... .

Super-Alchemy

Recall that "conventional alchemy" is the pseudoscientific predecessor of chemistry that sought a method for transmuting base metals into gold.

In this vein, seeking a theory that would transform ignorance and lack of information into "robust decisions" can be regarded an exponent of super-alchemy.

For, consider the basic facts:

  • The uncertainty we are dealing with is radical:

    • The uncertainty space can be vast (even unbounded).

    • The estimate we have is poor (can be a guess, even a wild guess).

    • The uncertainty model is likelihood-free.

  • We conduct an analysis in the neighborhood of the poor point-estimate.

  • We ignore the performance of decisions in areas of the uncertainty space that are at a distance from the estimate.

And yet, against all odds, and in violation of the Garbage In -- Garbage Out (GIGO) Axiom and its relations, we obtain decisions that are robust against radical uncertainty.

Doesn't this amount to super alchemy?

Fooled by rhetoric

Decision-making in the face of radical uncertainty is a formidable task, and developing a compressive theory for this task is even more demanding.

The authors' approach to this difficult task is to raise the level of rhetoric with the aid of words games.

That is, they take a model that was developed initially in 1996 (Ben-Haim (1996)) for the purpose of handling (small) perturbations in a given nominal value of a parameter, and elevate it -- by means of rhetoric -- to the level of a model for dealing with radical uncertainty. They then take this model, which is capable only of handling neighborhoods of a nominal value of the parameter of interest, and elevate it -- by rhetoric -- to the level of a model that (purportedly) determines the widest range of satisfactory outcomes associated with a given decision.

They then elevate this model --- known as a simple instance of the most famous model in the trade --- by means of rhetoric --- to the level of a new normative panacea for decision-making in the face of radical uncertainty.

But, the rhetoric cannot conceal the following simple facts about the proposed new theory:

  • The proposed robustness model is not new. It is a simple instance of the famous Radius of Stability model (circa 1960), and therefore an instance of the even more famous Wald's Maximin model (1940).

  • The proposed robustness model does not seek decisions with the widest range of satisfactory outcomes. It seeks decisions that maximize the size of the neighborhood around a poor estimate whose elements are satisfactory.

  • The proposed robustness model is utterly unsuitable for the treatment of radical uncertainty. The more radical the uncertainty, the more unsuitable the proposed model is.

  • Robustness models that maximize the range of satisfactory outcomes were proposed years ago (circa 1970). They are rarely used in practice because the optimization problems that they induce are usually extremely difficult to solve. So their application is restricted to highly specialized situations.

  • The proposed new theory does not address, let alone resolve, the difficult issues pertaining to deciding what constitutes a satisfactory ( 'good enough') outcome.

An explanation of the large font :

My "public" critique of info-gap decision theory goes back to the end of 2006. But some info-gap proponents prefer to avoid a direct reply to it. They prefer to spin their way around it.

This may have to do with the fact that I normally use normal font, so an increase in the size of the font may perhaps do the trick ....

I tried color before, but it did not work ...

So ..we shall have to wait and see.

State of the art

The article exhibits a total disrespect for the state of the art in the main topics discussed in the article.

One of the important traditions in academia is that a discussion on a topic engages with the facts that bear on it, even if these facts are not favorable to the ideas advanced in the discussion. It is equally customary to discuss both the capabilities and limitations of proposed methods, theories, procedures, etc.

But in this article, the authors do not even attempt to follow this long tradition. They portray a rosy picture of the proposed new theory completely ignoring its limitations and the critique that is directed at its various ingredients.

Consider for example the proposed robustness model, that is, info-gap's robustness model:

Formal proofs -- in peer-reviewed publications going back to 2007 -- demonstrate that this model is neither "new" nor "radically different", as claimed in the info-gap literature, but is rather a simple instance of Wald's famous Maximin.

But, there is no mention of this fact in the article.

Proofs -- in peer-reviewed publications going back to 2007 -- show that the proposed robustness model does not seek robustness against severe uncertainty, but rather against small perturbations in the nominal value of a parameter.

But, there is no mention of this fact in the article.

There are numerous peer-reviewed publications that question the validity of the thesis that "satisficing is better than optimizing".

But there is no mention of this fact in the article.

There is a thriving branch of optimization theory, called Robust Optimization that deals with robust decision-making problems of the type discussed in the article.

But, there is no mention of this fact in the article.

The upshot of all this is that the authors present as new a very simple instance of old and well established robustness models. Worse, the authors fail to advise the readers of the limitations of this model notably the fact that it deals with local rather than global robustness.

The authors thus depict a thoroughly distorted picture of the state of the art and the proposed theory.

What Next?

It will be interesting to see how long will proponents of info-gap decision theory continue to promulgate the myth that info-gap decision theory is a distinct, novel theory that is radically different from all current theories of decisions under uncertainty.

And it will be even more interesting to see how long will peer reviewed journals continue to accept publications that conceal from the public the Maximin and Radius of stability connections.

Of particular interest is the new myth about info-gap decision theory: its ability to maximize the range of satisfactory outcomes.

Because this myth asserts a real (scientific) miracle: a very simple mathematical model of local robustness has the capability to determine the widest range of satisfactory outcomes!

And this when, all these years (at least since the 1960s), this model has been used extensively in a range of fields (numerical analysis, optimization, control theory, stability theory, economics, operations research, and so on) only for the purpose of analyzing small perturbations in the nominal value of a parameter!

Imagine how much we lost as a result of so many scholars failing to identify the (miraculous) capabilities of this simple model!

But, as we say here, No Worries!!!

Other Reviews

  1. Ben-Haim (2001, 2006): Info-Gap Decision Theory: decisions under severe uncertainty.

  2. Regan et al (2005): Robust decision-making under severe uncertainty for conservation management.

  3. Moilanen et al (2006): Planning for robust reserve networks using uncertainty analysis.

  4. Burgman (2008): Shakespeare, Wald and decision making under severe uncertainty.

  5. Ben-Haim and Demertzis (2008): Confidence in monetary policy.

  6. Hall and Harvey (2009): Decision making under severe uncertainty for flood risk management: a case study of info-gap robustness analysis.

  7. Ben-Haim (2009): Info-gap forecasting and the advantage of sub-optimal models.

  8. Yokomizo et al (2009): Managing the impact of invasive species: the value of knowing the density-impact curve.

  9. Davidovitch et al (2009): Info-gap theory and robust design of surveillance for invasive species: The case study of Barrow Island.

  10. Ben-Haim et al (2009): Do we know how to set decision thresholds for diabetes?

  11. Beresford and Thompson (2009): An info-gap approach to managing portfolios of assets with uncertain returns

  12. Ben-Haim, Dacso, Carrasco, and Rajan (2009): Heterogeneous uncertainties in cholesterol management

  13. Rout, Thompson, and McCarthy (2009): Robust decisions for declaring eradication of invasive species

  14. Ben-Haim (2010): Info-Gap Economics: An Operational Introduction

  15. Hine and Hall (2010): Information gap analysis of flood model uncertainties and regional frequency analysis

  16. Ben-Haim (2010): Interpreting Null Results from Measurements with Uncertain Correlations: An Info-Gap Approach

  17. Wintle et al. (2010): Allocating monitoring effort in the face of unknown unknowns

  18. Moffitt et al. (2010): Securing the Border from Invasives: Robust Inspections under Severe Uncertainty

  19. Yemshanov et al. (2010): Robustness of Risk Maps and Survey Networks to Knowledge Gaps About a New Invasive Pest

  20. Davidovitch and Ben-Haim (2010): Robust satisficing voting: why are uncertain voters biased towards sincerity?

  21. Schwartz et al. (2010): What Makes a Good Decision? Robust Satisficing as a Normative Standard of Rational Decision Making

  22. Arkadeb Ghosal et al. (2010): Computing Robustness of FlexRay Schedules to Uncertainties in Design Parameters

  23. Hemez et al. (2002): Info-gap robustness for the correlation of tests and simulations of a non-linear transient

  24. Hemez et al. (2003): Applying information-gap reasoning to the predictive accuracy assessment of transient dynamics simulations

  25. Hemez, F.M. and Ben-Haim, Y. (2004): Info-gap robustness for the correlation of tests and simulations of a non-linear transient

  26. Ben-Haim, Y. (2007): Frequently asked questions about info-gap decision theory

  27. Sprenger, J. (2011): The Precautionary Approach and the Role of Scientists in Environmental Decision-Making

  28. Sprenger, J. (2011): Precaution with the Precautionary Principle: How does it help in making decisions

  29. Hall et al. (2011): Robust climate policies under uncertainty: A comparison of Info-­-Gap and RDM methods

  30. Ben-Haim and Cogan (2011) : Linear bounds on an uncertain non-linear oscillator: an info-gap approach

  31. Van der Burg and Tyre (2011) : Integrating info-gap decision theory with robust population management: a case study using the Mountain Plover

  32. Hildebrandt and Knoke (2011) : Investment decisions under uncertainty --- A methodological review on forest science studies.

  33. Wintle et al. (2011) : Ecological-economic optimization of biodiversity conservation under climate change.

  34. Ranger et al. (2011) : Adaptation in the UK: a decision-making process.

Recent Articles, Working Papers, Notes

Also, see my complete list of articles
    Moshe's new book!
  • Sniedovich, M. (2012) Fooled by local robustness, Risk Analysis, in press.

  • Sniedovich, M. (2012) Black swans, new Nostradamuses, voodoo decision theories and the science of decision-making in the face of severe uncertainty, International Transactions in Operational Research, in press.

  • Sniedovich, M. (2011) A classic decision theoretic perspective on worst-case analysis, Applications of Mathematics, 56(5), 499-509.

  • Sniedovich, M. (2011) Dynamic programming: introductory concepts, in Wiley Encyclopedia of Operations Research and Management Science (EORMS), Wiley.

  • Caserta, M., Voss, S., Sniedovich, M. (2011) Applying the corridor method to a blocks relocation problem, OR Spectrum, 33(4), 815-929, 2011.

  • Sniedovich, M. (2011) Dynamic Programming: Foundations and Principles, Second Edition, Taylor & Francis.

  • Sniedovich, M. (2010) A bird's view of Info-Gap decision theory, Journal of Risk Finance, 11(3), 268-283.

  • Sniedovich M. (2009) Modeling of robustness against severe uncertainty, pp. 33- 42, Proceedings of the 10th International Symposium on Operational Research, SOR'09, Nova Gorica, Slovenia, September 23-25, 2009.

  • Sniedovich M. (2009) A Critique of Info-Gap Robustness Model. In: Martorell et al. (eds), Safety, Reliability and Risk Analysis: Theory, Methods and Applications, pp. 2071-2079, Taylor and Francis Group, London.
    • .
  • Sniedovich M. (2009) A Classical Decision Theoretic Perspective on Worst-Case Analysis, Working Paper No. MS-03-09, Department of Mathematics and Statistics, The University of Melbourne.(PDF File)

  • Caserta, M., Voss, S., Sniedovich, M. (2008) The corridor method - A general solution concept with application to the blocks relocation problem. In: A. Bruzzone, F. Longo, Y. Merkuriev, G. Mirabelli and M.A. Piera (eds.), 11th International Workshop on Harbour, Maritime and Multimodal Logistics Modeling and Simulation, DIPTEM, Genova, 89-94.

  • Sniedovich, M. (2008) FAQS about Info-Gap Decision Theory, Working Paper No. MS-12-08, Department of Mathematics and Statistics, The University of Melbourne, (PDF File)

  • Sniedovich, M. (2008) A Call for the Reassessment of the Use and Promotion of Info-Gap Decision Theory in Australia (PDF File)

  • Sniedovich, M. (2008) Info-Gap decision theory and the small applied world of environmental decision-making, Working Paper No. MS-11-08
    This is a response to comments made by Mark Burgman on my criticism of Info-Gap (PDF file )

  • Sniedovich, M. (2008) A call for the reassessment of Info-Gap decision theory, Decision Point, 24, 10.

  • Sniedovich, M. (2008) From Shakespeare to Wald: modeling wors-case analysis in the face of severe uncertainty, Decision Point, 22, 8-9.

  • Sniedovich, M. (2008) Wald's Maximin model: a treasure in disguise!, Journal of Risk Finance, 9(3), 287-291.

  • Sniedovich, M. (2008) Anatomy of a Misguided Maximin formulation of Info-Gap's Robustness Model (PDF File)
    In this paper I explain, again, the misconceptions that Info-Gap proponents seem to have regarding the relationship between Info-Gap's robustness model and Wald's Maximin model.

  • Sniedovich. M. (2008) The Mighty Maximin! (PDF File)
    This paper is dedicated to the modeling aspects of Maximin and robust optimization.

  • Sniedovich, M. (2007) The art and science of modeling decision-making under severe uncertainty, Decision Making in Manufacturing and Services, 1-2, 111-136. (PDF File) .

  • Sniedovich, M. (2007) Crystal-Clear Answers to Two FAQs about Info-Gap (PDF File)
    In this paper I examine the two fundamental flaws in Info-Gap decision theory, and the flawed attempts to shrug off my criticism of Info-Gap decision theory.

  • My reply (PDF File) to Ben-Haim's response to one of my papers. (April 22, 2007)

    This is an exciting development!

    • Ben-Haim's response confirms my assessment of Info-Gap. It is clear that Info-Gap is fundamentally flawed and therefore unsuitable for decision-making under severe uncertainty.

    • Ben-Haim is not familiar with the fundamental concept point estimate. He does not realize that a function can be a point estimate of another function.

      So when you read my papers make sure that you do not misinterpret the notion point estimate. The phrase "A is a point estimate of B" simply means that A is an element of the same topological space that B belongs to. Thus, if B is say a probability density function and A is a point estimate of B, then A is a probability density function belonging to the same (assumed) set (family) of probability density functions.

      Ben-Haim mistakenly assumes that a point estimate is a point in a Euclidean space and therefore a point estimate cannot be say a function. This is incredible!


  • A formal proof that Info-Gap is Wald's Maximin Principle in disguise. (December 31, 2006)
    This is a very short article entitled Eureka! Info-Gap is Worst Case (maximin) in Disguise! (PDF File)
    It shows that Info-Gap is not a new theory but rather a simple instance of Wald's famous Maximin Principle dating back to 1945, which in turn goes back to von Neumann's work on Maximin problems in the context of Game Theory (1928).

  • A proof that Info-Gap's uncertainty model is fundamentally flawed. (December 31, 2006)
    This is a very short article entitled The Fundamental Flaw in Info-Gap's Uncertainty Model (PDF File) .
    It shows that because Info-Gap deploys a single point estimate under severe uncertainty, there is no reason to believe that the solutions it generates are likely to be robust.

  • A math-free explanation of the flaw in Info-Gap. ( December 31, 2006)
    This is a very short article entitled The GAP in Info-Gap (PDF File) .
    It is a math-free version of the paper above. Read it if you are allergic to math.

  • A long essay entitled What's Wrong with Info-Gap? An Operations Research Perspective (PDF File) (December 31, 2006).
    This is a paper that I presented at the ASOR Recent Advances in Operations Research (PDF File) mini-conference (December 1, 2006, Melbourne, Australia).

Recent Lectures, Seminars, Presentations

If your organization is promoting Info-Gap, I suggest that you invite me for a seminar at your place. I promise to deliver a lively, informative, entertaining and convincing presentation explaining why it is not a good idea to use — let alone promote — Info-Gap as a decision-making tool.

Here is a list of relevant lectures/seminars on this topic that I gave in the last two years.

Disclaimer: This page, its contents and style, are the responsibility of the author (Moshe Sniedovich) and do not represent the views, policies or opinions of the organizations he is associated/affiliated with.


Last modified: