| Reference: |
Y. Ben-Haim, M. Zacksenhouse, C. Keren, C.C. Dacso Do we know how to set decision thresholds for diabetes? Medical Hypotheses, Volume 73, Issue 2, Pages 189-193, 2009 |
| Abstract | The diagnosis of diabetes, based on measured fasting plasma glucose level, depends on choosing a threshold level for which the probability of failing to detect disease (missed diagnosis), as well as the probability of falsely diagnosing disease (false alarm), are both small. The Bayesian risk provides a tool for aggregating and evaluating the risks of missed diagnosis and false alarm. However, the underlying probability distributions are uncertain, which makes the choice of the decision threshold difficult. We discuss an hypothesis for choosing the threshold that can robustly achieve acceptable risk. Our analysis is based on info-gap decision theory, which is a non-probabilistic methodology for modelling and managing uncertainty. Our hypothesis is that the non-probabilistic method of info-gap robust decision making is able to select decision thresholds according to their probability of success. This hypothesis is motivated by the relationship between info-gap robustness and the probability of success, which has been observed in other disciplines (biology and economics). If true, it provides a valuable clinical tool, enabling the clinician to make reliable diagnostic decisions in the absence of extensive probabilistic information. Specifically, the hypothesis asserts that the physician is able to choose a diagnostic threshold that maximizes the probability of acceptably small Bayesian risk, without requiring accurate knowledge of the underlying probability distributions. The actual value of the Bayesian risk remains uncertain. |
| Acknowledgement | This work was supported in part by a Grant from the Abramson Center for the Future of Health, Houston, TX. |
| Scores | TUIGF:100% SNHNSNDN:100% GIGO:200% |
Since the idea of regarding Info-Gap's robustness model as a "proxy" for a probabilistic model of "success" had already been raised in a number of Ben-Haim's publications, I shall first examine how it sits in the general context of Info-Gap decision theory. Then, I shall examine it in some detail to see how it fares with regard to the specific Info-Gap model discussed in the paper.
Overview
Let us begin by noting that the journal Medical Hypotheses is devoted to the publication of ... medical hypotheses. According to its Guidelines for Authors:
The purpose of Medical Hypotheses is to publish interesting theoretical papers. The journal will consider radical, speculative and non-mainstream scientific ideas provided they are coherently expressed.
So, the question is: does the hypothesis proposed in the article fit the bill? Is it indeed radical and non-mainstream? And if so, in what sense is it radical and non-mainstream?
To work out an answer to this question you need not bother to read the paper in its entirety. The answer stares you in the face ... in the abstract, where we read (emphasis is mine):
Our analysis is based on info-gap decision theory, which is a non-probabilistic methodology for modelling and managing uncertainty. Our hypothesis is that the non-probabilistic method of info-gap robust decision making is able to select decision thresholds according to their probability of success.
The main objective of this review is to show that the proposition made by this hypothesis is not just "radical and non-mainstream", it is in fact unscientific, or more accurately counter-scientific. And to be able to appreciate why this is so keep in mind that Info-Gap's robustness model is by definition local and that the uncertainty that this model is designed to take on is severe.
So the good news is that the future of probability theory and statistics is not in danger ... not yet!
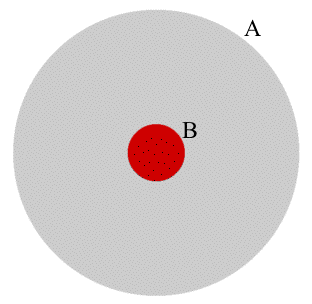In greater detail, consider the two circles, A and B on the left. The large circle represents the space that affects the choice and ranking of decisions according to their probability of success. The much smaller circle, B, represents the space that affects the choice and ranking of decisions as prescribed by Info-Gap's robustness analysis.
That B is typically a relatively small subset of A is a direct consequence of Info-Gap's local robustness analysis being conducted only on an infinitesimally small area of the (unbounded) uncertainty space (A) that Info-Gap decision theory presumably takes on.
So mathematically speaking we can look at the proposed hypothesis as being grounded in a comparison between the results yielded by two algorithms: one is defined on A, call it f, and one is defined on B, call it g. Algorithm f yields the ranking of decisions according to their probability of success, whereas Algorithm g yields the ranking of decisions according to their robustness (as prescribed by Info-Gap).
The authors' hypothesis is that these two algorithms yield the same results.
But the point to note here is that for this hypothesis to hold, Algorithm g must exhibit a significant level of redundancy and/or degeneracy. However, since redundancy and/or degeneracy is not a generic characteristic of the probabilistic models of "success" examined by the authors, the inference is that this must be imposed on the two models through certain assumptions that would link the performance of the two algorithms.
Since the authors do not postulate any such assumptions, there is no reason to believe that the proposed hypothesis is valid.
To the contrary, there is every reason to believe that in the absence of some inherent redundancy/degeneracy in the specific probabilistic model of success examined in the article, this hypothesis cannot hold. It is simply too good to be true: how can a non-probabilistic analysis of a small subset of a much large set be a reliable proxy for a probabilistic analysis of "success" over the much larger set?
Indeed, if we accept this "too good to be true" hypothesis, why not accept "too good to be true" offers such as this:
Date: Sun, 7 Jun 2009 01:47:13 +0200 (MEST) From: ??????? Reply-To: ??????? Subject: My Friend My Friend How are you today? Hope all is well with you and your family? I am using this opportunity to inform you that this multi-million-dollar business has been concluded with the assistance of another partner from Chile who financed the transaction to a logical conclusion. Due to your effort,sincerity courage and trust worthiness You showed during the course of the transaction. I have left a certified Bank Draft. for you worth of $1,300,000.00 cashable anywhere in the world. Mr. ??????
The absurd in the proposed hypothesis is on a par with the absurd in the proposition that what you see through a keyhole is a reliable proxy of what you see through an open door.
 |
vs |
Hide/Show the BIG picture!
|
As they say: never believe what you see through a keyhole!
And if you like cheese, then perhaps the following analogy will be more meaningful to you:
 |
vs |
Hide/Show the BIG picture!
|
Perhaps.
One of the most impressive illustrations of this point is no doubt this:
 |
vs |
Hide/Show the BIG picture!
|
Commonly known as "the tip of the iceberg".
However, to my mind, the most edifying analogy is the distinction between a local and a global optimum.
 |
vs |
Hide/Show the BIG picture!
|
As we well know, generally, a local optimum is not necessarily a global optimum. Indeed, we go to great lengths to explain to our students why it is important to avoid confusing between these two related concepts.
A similar distinction between local and global robustness of course applies in the case of Info-Gap. But we find no trace of it in the Info-Gap literature. To wit:
- Info-Gap's rhetoric promises a global robustness against severe uncertainty,
whereas
- Info-Gap's robustness analysis delivers a local robustness in the neighborhood of a wild guess.
Worse, not only is there no awareness whatsoever, in the Info-Gap literature, of the difference between these two types of robustness, there is no awareness of the fact that the robustness yielded by Info-gap is local.
And to top it all off, Info-Gap scholars persistently fail (or avoid) to indicate that Info-Gap's robustness model is in fact a simple instance of Wald's famous Maximin model (circa 1940). Meaning that the Info-Gap analysis is in fact a (local) worst-case analysis.
In a word, only a failure to appreciate the distinction between global and local robustness could have inspired this hypothesis.
Illustrative example
Suppose that robustness is sought with respect to the constraint f(x) ≥ 0 over the set X=[-7,7], where f is the function shown below:
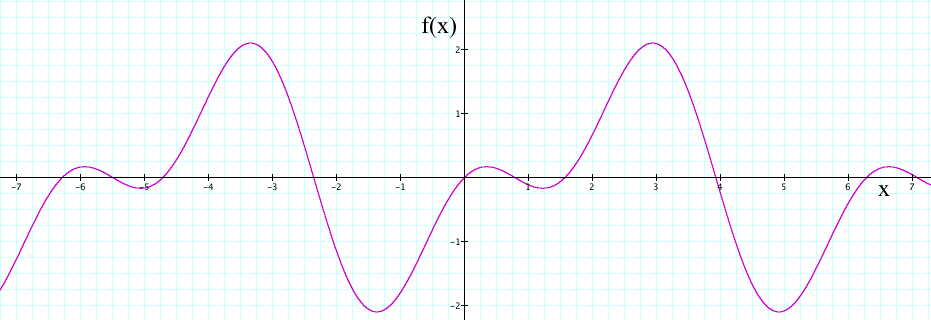
If x is the realization of a random variable, we can consider the probability that f(x) ≥ 0 as a measure of robustness. In this case this probability is the probability that the random variable takes value in the blue intervals shown below:
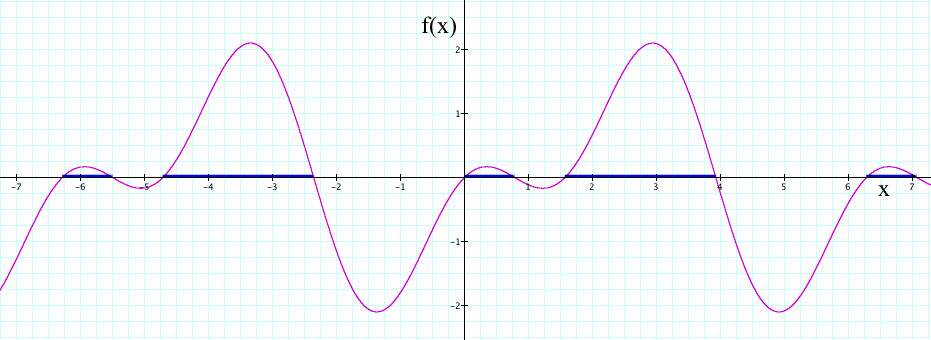
If the probability distribution of this random variable is known, then it would be a simple task to compute the probability that f(x) ≥ 0.
But what should we do if we face severe uncertainty and we do not know the distribution of this random variable?
The hypothesis proposes that Info-Gap's non-probabilistic robustness model can be used as a proxy for obtaining the unknown probability distribution.
To apply this model we shall have to estimate the "true" value of x and conduct the robustness analysis in the neighborhood of this estimate, call it x*. For instance, if we assume that x*=3, we shall conduct the robustness analysis in the interval, say [1.5,4], as shown below:
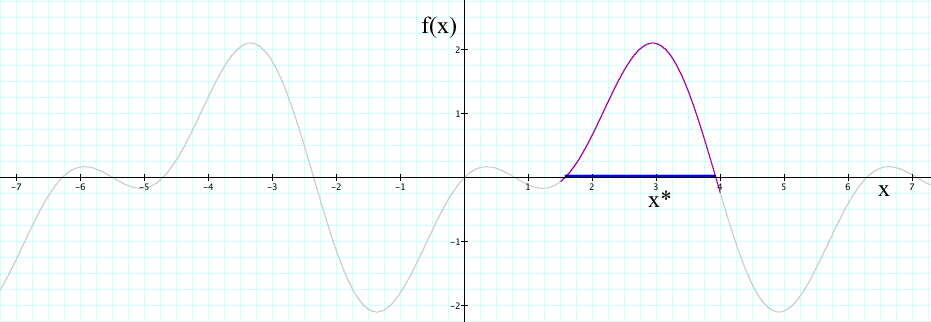
So in this case the hypothesis is that Info-Gap's local robustness analysis in the interval X'=[1.5,4] will yield a reliable proxy for the probability of f(x) ≥ 0 over the interval X=[-7,7].
In short, if we accept that the hypothesis has any merit whatsoever, we must accept that Info-Gap's robustness model is endowed with substantial extraordinary powers. Namely, we must accept that it has the capability to generate reliable probabilistic results out of a non-probabilistic model of uncertainty, and all this by means of a local analysis in the neighborhood of a poor estimate!
This is too good to be true!
Reality Check
So, to set the record straight on the proposition that Info-Gap robustness is a reliable proxy for the probability of success, consider the following formal result:
Reality Check Theorem:The proposed hypothesis is not valid.
That is, consider the generic Info-Gap robustness model
α(q,û):= {α≥0: R(q,u) ≤ Rc , ∀u∈U(α,û)} , q∈Q and assume that α(q'',û) > α(q',û) for some decisions q' and q'' in Q. Then this does not imply that Pr[R(q'',u) ≤ Rc] > Pr[R(q',u) ≤ Rc], where Pr[event] denotes the probability of "event" as determined by some (unknown) probability distribution on the uncertainty space U.
Proof.
It is sufficient to show that there are cases where for some decisions q' and q'' such that α(q'',û) > α(q',û) there is a probability distribution on U such that Pr[R(q',u) ≤ Rc] > Pr[R(q'',u) ≤ Rc].
Let
D(q',q''):= {u∈U: R(q',u) ≤ Rc; R(q'',u)> Rc} By definition then, D(q',q'') denotes the subset of U on which decision q' satisfices the performance requirement and decision q'' violates this requirement.
Now consider any case where D(q',q'') is not empty. Then clearly, there is a probability distribution on U such that Pr[R(q',u) ≤ Rc] > Pr[R(q'',u) ≤ Rc]. For example, any distribution whose support is a subset of D(q',q'') will do the job. QED
Clearly then, the proposed hypothesis does not hold in the context of Info-Gap's generic robustness model.
Our next task is to explain the fundamental flaws in the thinking behind the hypothesis.
Garbage In — Garbage Out Axiom
The question that we need to ask ourselves is as follows:
How is it possible that a methodology employing a non-probabilistic model of uncertainty is capable of selecting decisions according to their probability of success?
The short answer is clear:
Either this hypothesis is groundless, or ... there exist certain implicit powerful links between the probabilistic and non-probabilistic models that empower the latter to mimic the behavior of the former.
Regarding the second option, see for example the well known concept deterministic equivalent that is used extensively in stochastic programming. All that needs to be pointed out here is that, the existence of deterministic equivalent models relies on the validity of very strong assumptions.
The longer answer is as follows:
Either this hypothesis is groundless, or ... there exist certain implicit powerful links between the probabilistic and non-probabilistic models that empower the latter to mimic the behavior of the former.It does not take much to explain why this hypothesis is groundless with regard to Info-Gap's robustness model. Because, to claim that this hypothesis is valid for Info-Gap's robustness model, without invoking the support of certain prerequisite assumptions, is as good as declaring in public that the universally accepted Garbage In -- Garbage Out (GIGO) Axiom is null and void.
But in this case Info-Gap decision theory puts itself at loggerheads with "Conventional Science" as follows:
Conventional Science Info-Gap Decision Theory
wild guess -----> Model -----> wild guess
wild guess -----> Model -----> reliable
robust decision
That is, in science the ruling convention is that results generated by a model can be only as good as the estimate on which they are based. Yet, Info-Gap decision theory proclaims its robustness model capable of generating reliable robust decisions by an analysis of the neighborhood of a wild guess of the true value of the parameter of interest. Namely, without bothering to give the slightest justification, Info-gap attributes extraordinary powers to its robustness model, to reliably extrapolate from local results in a small neighborhood of a wild guess to the entire vast uncertainty space U.
In short, by contravening the Garbage In -- Garbage Out Axiom, Info-Gap decision theory is at odds with a fundamental precept of science thereby showing itself to be an unscientific theory. Therefore, the very idea of proposing such an hypothesis is of a piece with the voodoo (counter-scientific) approach taken by Info-Gap to decision- making under uncertainty.
It is apposite to add here that if we accept for a fact Info-Gap's extraordinary ability to generate reliable robust decisions out of a wild guess, then we may as well wind up the discipline of Decision Making Under Severe Uncertainty and declare it redundant. For, dealing with decision-making problems subject to severe uncertainty would now amount to child's play:
1-2-3 fool-proof recipe for decision-making under severe uncertainty
- Ignore the severity of the uncertainty.
- Focus instead on the neighborhood of your best estimate of the parameter of interest.
- Don't worry if you lack an estimate, a wild guess will do*.
Wouldn't this be great?!
*Should you need it, the recipe for obtaining a wild guess is simplicity itself:
- Wet your index finger and put it in the air.
- Think of a number and double it.
See it on-line at wiki.answers.com/Q/What_is_best_estimate_and_how_do_i_calculate_it.
The Hypothesis
Given the state of the art in decision theory and robust optimization, what we have here is
Eithera major breakthrough in decision theory and robust optimization!Or,a huge blunder attesting to a fundamental misapprehension/misconception of the central difficulty confronting decision-making in the face of severe uncertainty.
So, to repeat the obvious:
The basic difficulty facing decision-making under severe uncertainty is that the estimate we have of the true value of the parameter of interest is poor and likely to be substantially wrong. Hence, there is no reason to believe that a local analysis in the neighborhood of the estimate will yield reliable results.The question is then: what should be done given this state of affairs?!
In a nutshell, the severity of the uncertainty makes a global treatment of robustness imperative. That is, it demands that the entire uncertainty space, or a suitable global approximation thereof, be explored.
Here then are two simple reasons why the proposed hypothesis is groundless:
- Info-Gap's robustness analysis is not conducted over the entire specified uncertainty space.
- In the framework of Info-Gap decision theory, the estimate used is a wild guess and is likely to be substantially wrong.
So, the question is: how can the proposed hypothesis have any merit whatsoever when Info-Gap's robustness model itself (before you even begin to ponder the hypothesis) is fundamentally flawed? And the answer is plain: for the hypothesis to hold, not only is it imperative that extremely stringent conditions hold to establish the envisaged powerful nexus between Info-Gap's robustness model and the probabilistic model of "success". It is imperative that the model itself be sound. Since no such conditions are incorporated on the (already fundamentally flawed) generic Info-Gap robustness model, it is not surprising that the hypothesis is generally not valid.
By the same token, given that no such conditions are imposed on the models presented in the paper, it follows that there is no reason to believe that the hypothesis can hold for these models.
To examine this contention more formally, assume that the performance constraint is defined as follows:
R(q,u) ≤ Rc
where q represents the decision variable, u represent the parameter of interest, R represents the performance functions and Rc denotes the required performance level.
In this framework, the probability of success is
PrU[R(q,u) ≤ Rc]
where PrU[event] denotes the probability of "event". The subscript U is used as a reminder that the probability is computed over the uncertainty space U, namely the set of possible values of u.
So far so good.
Now, according to Info-Gap decision theory, the robustness of decision q is defined as follows:
α(q,û):= max {α: R(q,u) ≤ Rc , ∀u∈U(α,û)}
where û denotes the estimate of the true value of u and U(α,û) denotes a region of uncertainty of size α around û.
So, the main thesis of this paper is as follows:
Hypothesis:
α(q'',û) > α(q',û) ————> PrU[R(q'',u) ≤ Rc] > PrU[R(q',u) ≤ Rc]
In words: if Info-Gap's analysis deems decision q'' to be more robust than decision q', then q'' has also a greater probability of success (satisficing the performance requirement).
Some Basic Facts
Before we subject the proposed hypothesis to a formal analysis, let us list the basic facts about Info-Gap's robustness analysis and its relationship to a probabilistic model of success:
- Fact 1: The probability of success, namely PrU[R(q,u) ≤ Rc], is determined by a probability distribution over the entire region of uncertainty U so that potentially it hangs on the performance of decision q relative to the entire region U. The key point is that the probability of success is a global property insofar as U is concerned. The picture is this:
û - Fact 2: Info-Gap's robustness analysis is conducted in the neighborhood of a point estimate of the parameter of interest. So generally, Info-Gap's robustness analysis is completely oblivious to the performance of decision q in large regions of U. This is particularly striking if U is unbounded. The key point is that "Info-Gap robustness" is a local property insofar as U is concerned. The picture is this:
No Man's Land û No Man's Land - Fact 3: Under severe uncertainty, the point estimate is a wild guess of the true value of u and is likely to be substantially wrong. The picture is this:
No Man's Land û No Man's Land u* where u* denotes the true value of u.
- Fact 4: There are no grounds whatsoever to proceed from an assumption that it is highly probable that the true value of u is in the immediate value of û. In fact, given the severity of the uncertainty assumed by Info-Gap decision theory, there is no reason to believe that the probability of u over U has high peaks.
We are now ready for a formal examination of the proposed hypothesis.
Anatomy of an Hypothesis
To examine the hypothesis more closely, consider the following three general obvious observations:
- It is straightforward to show — by means of a simple counter example — that this hypothesis is in general invalid, namely that situations exist where the hypothesis does not hold.
- It is straightforward to show — prove formally — that the hypothesis is valid for some trivial degenerate cases.
- It is extremely easy to conduct numerical experiments in the framework of the specific application considered in the paper (maximizing the probability of a correct diagnosis of diabetes), so as to put this hypothesis to the test.
So, let us now examine each observation in greater detail.
Counter Example
Consider the case shown in the following picture:
Info-Gap decision theory deems q'' to be more robust, but it is clear that q' dominates q'' over most of the uncertainty space U=ℜ. The dark areas at the bottom of the picture show the regions of U where the constraint is satisfied by these two decisions.
So, there are no too ways about it, q' is far more robust than q'' relative to the complete uncertainty space U.
It follows then that if the probability of u is not "concentrated" in the two very small intervals where q'' dominates q', the hypothesis is not valid. For example, if PrU[u∈U(α(q'',û)] is sufficiently small, then clearly the hypothesis does not hold.
Degenerate Valid Example
It can be shown (see FAQ # 62) that in some trivial degenerate cases Info-Gap's robustness in the neighborhood of an estimate — even a very bad one — is a "proxy" for the true robustness over the entire uncertainty space U. In such cases — which are of little interest, if any — the hypothesis is valid regardless of the specific structure of the probabilistic model, namely PrU[event]. However, as explained in FAQ # 62, in these cases there is no need for the Info-Gap model in the first place. The results can be obtained directly from the performance constraint. The estimate û is just a nuisance parameter.
Numerical Experiments
The specific Info-Gap robustness model studied in the paper is so simple that closed-form solutions are readily available. Meaning that, it is extremely easy to test this hypothesis by conducting numerical experiments via simulation. It is unclear, therefore, why the authors did not bother to do this in order to see whether the hypothesis can have any merit.
The "Why is the hypothesized plausible?" section
For obvious reasons the Journal requires that contributors explain why the radical hypotheses that they propose are plausible. This is done under the heading "Why is the hypothesized plausible?".
In this section of their paper the authors argue that their hypothesis is plausible because their Info-Gap analysis is based on two assumptions (page 4):
The info-gap models of uncertainty which underlie our example, Eqs. (5) and (6), assume two things: (i) that the cumulative distribution functions (CDFs) are normal (Gaussian) and (ii) that the estimated moments deviate fractionally by an unknown amount.
They then proceed to argue that these assumptions are reasonable.
But the hypothesis is not just about the Info-Gap models proposed in the article. The whole point of the hypothesis is that it makes a statement about a relationship between Info-Gap's robustness model and a probabilistic model of "success". So what should have been discussed under this heading is the plausibility of the assumed kinship between these two models.
So as the readers cannot possibly gather this from this article, it is important to take note that contrary to the local analysis that is prescribed by Info-Gap's local robustness model, the probability of success is detemined by a global expectation operator over the entire uncertainty space U.
The picture is this:
 |
Let A = U and B = U(α*,û). Since the authors assume that U is unbounded, B is actually an infinitesimally small subset of A. For illustrative purposes it is enlarged in this picture. Things to remember:
|
Given that the black dot is a wild guess of the white square, to argue that an analysis of the small white circle is a proxy of an analysis of the entire green island is tatamount to practicing voodoo science.
In a nutshell, this glaring incongruity between Info-Gap's robustness model and models determining the probability of success not only brings out the implausibility of this hypothesis. It brings out that the hypothesis in fact violates the universally accepted GIGO Axiom.
Conclusions
- The idea behind the proposed hypothesis is misguided: it asserts — without invoking relevant assumptions — that a local deterministic model yields the same results as a global probabilistic model.
- Unless stringent conditions are postulated to hold for the problem in question, there is no reason to believe that a local analysis in the neighborhood of a wild guess will yield a reliable result. This is precisely what the universally accepted GIGO Axiom dictates.
- Since no such conditions are postulated by the authors to hold for the specific problem under consideration, the authors' hypothesis is without any foundation.
- The comments in Review 6 and Review 9 regarding the likelihood-free nature of Info-Gap's robustness model are also relevant here.
- Ben-Haim (2009) discusses in detail the type of strong conditions that must be imposed (jointly) on the probability model and on Info-Gap's robustness model to justify the validity of the hypothesis.
It is therefore puzzling that no such conditions are discussed by the authors in this paper. Even more puzzling is the fact that the authors fail to cite Ben-Haim's (2009) paper and the results presented there regarding the connection between Info-Gap's robustness model and the probability of "success".
In short, we conclude that the future of probability theory and statistics ... is not in jeopardy ... not yet!
Recommendation
In view of the above, I strongly recommended that Medical Hypothesis require authors to indicate clearly in their papers whether the hypotheses that they propose withstand the test of the GIGO Axiom. If this cannot be done, then an explanation should be provided.
Stay tuned ... there is more in store!
And something to think about in the meantime:
The authors use an unbounded uncertainty space. This means, among other things, that they assume that the fasting plasma glucose (FPG) concentration can be arbitrarily low and high!According to the information available to me
- A FPG concentration below 2 (mmo/l) is extremely low and there is a danger of unconciousness.
- A FPG concentration above 30 (mmo/l) indicates a high danger of severe electrolyte imbalance.
- Apparently some meters/strips cannot read FPG concentrations above 35 (mmo/l).
So isn't it safe to assume that the only relevant FPG concentrations are in the range, say [0,50] (mmo/l) rather than the impressive unbounded range (-∞,∞) used by the authors? Do you know anyone — alive or otherwise — with negative FPG concentration?
Any comments/suggestions on this issue will be greatly appreciated!
Note: a mole is approximately 6.022141796*1023 molecules, and mmol/l = millimoles/liter. For blood glucose, the conversion from molecular count to weight is: mmol/l = 18 mg/dl (milligrams/deciliter).
