The Spin Stops Here!
Decision-Making Under Severe Uncertainty  
Faqs | Help | @ | Contact | home  
voodoostan info-gap decision theory info-gap economics severe uncertainty mighty maximin robust decisions responsible decisions

Tutorial: A Guided Tour of Info-Gap's Robustness Analysis and some of its Fundamental Flaws

Last modified: Sunday, 31-May-2009 17:15:35 MST

G'day and welcome to our guided tour of Info-Gap's Robustness Analysis:

This short tutorial is a supplement to my analysis of Info-Gap decision theory. Its main goal is to set the record straight on a number of myths that are advanced in the Info-Gap literature, notably that this theory provides a reliable recipe for tackling severe uncertainty.

The emphasis is on the conceptual foundation of Info-Gap's robustness model rather than on its technical aspects which are discussed in detail in FAQs about Info-Gap Decision Theory.

Very broadly, the objective here is to make vivid how Info-Gap's blatant violation of the universally accepted Garbage In -- Garbage Out (GIGO) Axiom, renders it a classic example of a voodoo decision theory. Namely, the objective is to show that Info-Gap's robustness evaluation relies on credence being given to a wild guess of the true value of the parameter of interest and on an analysis that is based entirely on such a wild guess and its neighborhood.

The argument is then that the results (output) yielded by such an analysis are necessarily on par with the (input) wild guess that they are based on. And hence, that any claims attributing Info-Gap's robustness model the ability to yield reliable/robust decisions in the face of severe uncertainty in the true value of the parameter, are in contravention of the Garbage In — Garbage Out (GIGO) Axiom and therefore without any merit.

This tutorial illustrates then the absurd in proposing Info-Gap's robustness model as a methodology for decision-making in the face of severe uncertainty.

Table of contents

Overview

Before we can embark on this tour we must first take care of a number of preliminaries. To begin with, we need to recall how the concept "robustness" enters the picture in decision-making, notably decision-making under severe uncertainty. And to do this we must first recall what the term "robustness" is understood to connote.

Observe then that according to WIKIPEDIA:

Robustness is the quality of being able to withstand stresses, pressures, or changes in procedure or circumstance. A system, organism or design may be said to be "robust" if it is capable of coping well with variations (sometimes unpredictable variations) in its operating environment with minimal damage, alteration or loss of functionality.

Granting then that the gist of the concept "robustness" is the ability to cope well with change, it is obvious why decision-making, especially under severe uncertainty, should be sought to be based on such a criterion. Clearly, the aspiration here is that the ability to pass a robustness test should deem decisions to be meaningful/worthwhile/sound. The question, of course, is what kind of test should decisions be subjected to in order to be deemed robust. Furthermore, how would this test be defined formally? In a word, what exactly is a "robust" solution to a decision-making problem?

And to go back to Info-Gap decision theory, here the question is not just what kind of test must a decision withstand in order to be deemed robust. The real question is what kind of test must a decision withstand in order to be deemed robust against severe uncertainty. That is, in the case of Info-Gap, the guiding idea must be that the definition of robustness should be meaningful/apposite/sound for decision-making in the face of severe uncertainty.

That this must be so is born out by the testimony of its founder. For, according to this testimony, Info-Gap decision theory was invented precisely with this objective in mind: to provide a methodology for decision-making under severe uncertainty. This, of course, is further amplified by the subtitles of both editions of the book on Info-Gap decision theory: "decisions under severe uncertainty".

But the whole point about Info-Gap decision theory is that it provides the wrong test for robustness against severe uncertainty. Namely, its robustness analysis is the precise antithesis of what a robustness analysis to severe uncertainty ought to be.

The trouble is that this fact is lost on unwary readers of the Info-Gap literature, because its phraseology and rhetoric on "ROBUSTNESS" are utterly confusing, indeed misleading. The term that should have been used from the outset is LOCAL robustness, to connote the same idea conveyed by "local" in local optimum, as opposed to "global" in global optimum.

And to illustrate, the picture on the right displays two local minima and one local maximum. If the function continues its ascent in both directions, then there would be only one global minimum and no global maximum. Recall that a global optimum is a local optimum, but a local optimum is not necessarily a global optimum.

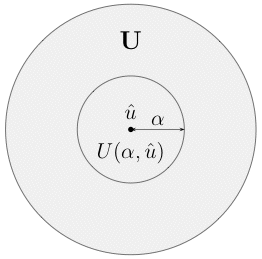
My point is then that an analogous distinction between local and global robustness is essential to any (sound) robustness analysis, especially in the face of uncertainty, but that such a distinction is nonexistent in Info-Gap decision theory. This failure is at its core, so that it cannot be corrected. Therefore, readers of the Info-gap literature should take note that this fundamental flaw is obscured by a rhetoric that conceals the huge gulf between Info-Gap's pronouncements on robustness and its capabilities. Namely:

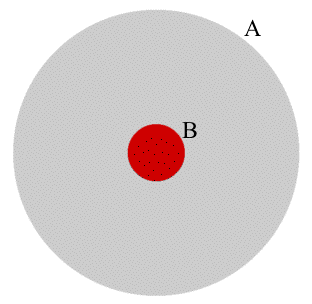
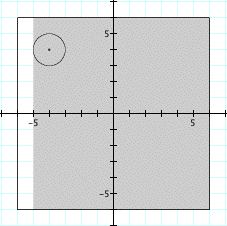
  • Info-Gap's rhetoric promises global robustness against severe uncertainty.

  • Info-Gap's robustness model delivers a local robustness in the neighborhood of a poor estimate.

The distinction between local and global robustness is similar to the distinction between local and global optima. That is, local robustness is a robustness with repsect to a neighborhood of a given point in the given uncertainty space, whereas global robustness is robustness with respect to the entire given uncertainty space.

The large circle (A) represents the given uncertainty space and the small circle (B) represents the subset thereof on which Info-Gap's local robustness analysis is conducted.

For obvious reasons we term the area of A that is outside B No Man's Land, to indicate that Info-Gap's robustness analysis is utterly unaffected by what occurs in this part of the uncertainty space.

To appreciate why this fact is detrimental to Info-Gap decision theory, it is important to keep in mind that Info-Gap decision theory is being advanced as a theory for decision-making in the face of severe uncertainty.

Severe Uncertainty

Although the term "severe uncertainty" is not given a precise formal definition by Info-Gap decision theory, three things are crystal clear:

  1. Info-Gap's uncertainty model is non-probabilistic and likelihood-free.

  2. The estimate of the parameter of interest employed by Info-Gap's uncertainty model is

    • a wild guess,

    • a poor indication of the true value of the parameter,

    • likely to be substantially wrong.

  3. Info-Gap decision theory is touted as a method capable of dealing with unbounded uncertainty spaces. Indeed, these cases are claimed to be commonly encountered in applications of the theory.

So it is against this kind of uncertainty that Info-Gap's robustness analysis must be interpreted, evaluated, and judged.

To be able to give a clear and precise picture of Info-gap's mode of operation and its consequences, let:

In the framework of Info-Gap decision theory, all we know is that u* and û are elements of U and that there are no grounds to believe that u* is "close" to û. Methodologically then, the picture is this:

 û u*

where the black area represents the uncertainty space U.

Given that Info-Gap's uncertainty model is non-probabilistic and likelihood-free, there are no grounds whatsoever to assume that u* is more/less likely to be located in any one particular neighborhood of U. Hence, there is no reason to believe that u* is located close to û.

So while we may not have in hand a fully formed idea of how to define robustness against severe uncertainty of this kind, one thing is crystal clear. For robustness to have any merit whatsoever in this environment, it cannot possibly be local. In other words, it is utterly senseless to define robustness against uncertainty of this nature in terms of what happens in a small subset of U.

For instance, suppose that we decide to

Then the picture will be as follows:

 û u*

where the red area around the estimate represents the subset of U with respect to which robustness is defined.

The point to note then is that such a formula for obtaining robustness against severe uncertainty of the kind addressed by Info-Gap decision theory is not just erroneous. It is so incongruent with the whole notion of severe uncertainty and the difficulties posed by it, that one wonders how such a formula can even be contemplated!

Illustrative Example

Suppose that robustness is sought with respect to the constraint R(q,u) ≥ 0 over the set U=[-7,7], where q denotes a decision and R(q,u) denotes the performance level of decision q if the true value of the parameter of interest is equal to u.

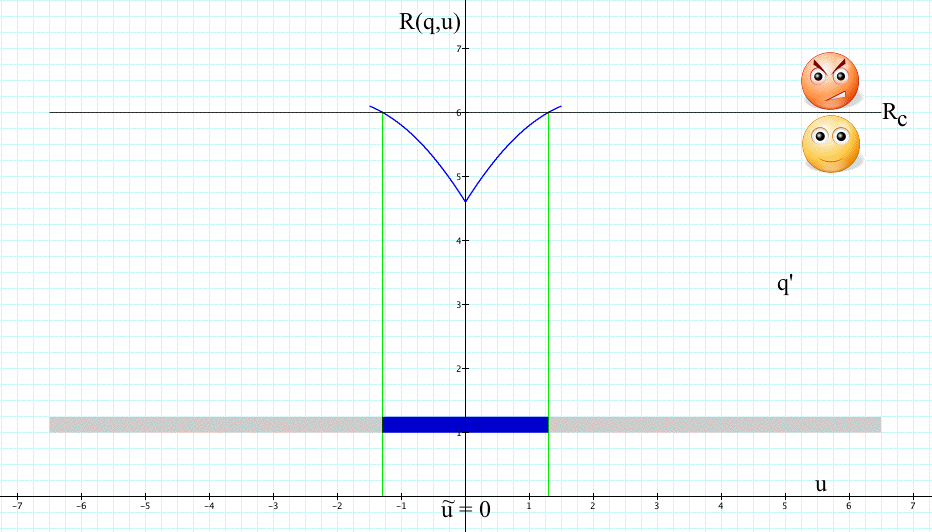
The regions where this requirement is satisficed are shown below:

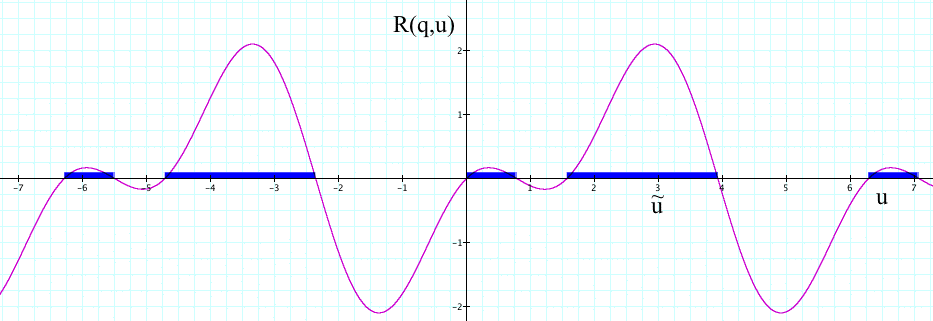
To use Info-Gap decision theory, we must first estimate the "true" value of u and conduct the robustness analysis in the neighborhood of this estimate, call it û. For instance, if we assume that û=3, we shall conduct the robustness analysis in the interval, say U'=[1.5,4], as shown below:

The robustness of q is defined by Info-Gap decision theory as the "size" of the region around the estimate û over which the performance constraint is satisfied.

The claim is then that the performance of decision q in the neighborhood U'=[1.5,4] of the poor estimate û is indicative of its performance over the entire region of uncertainty U=[-7,7].

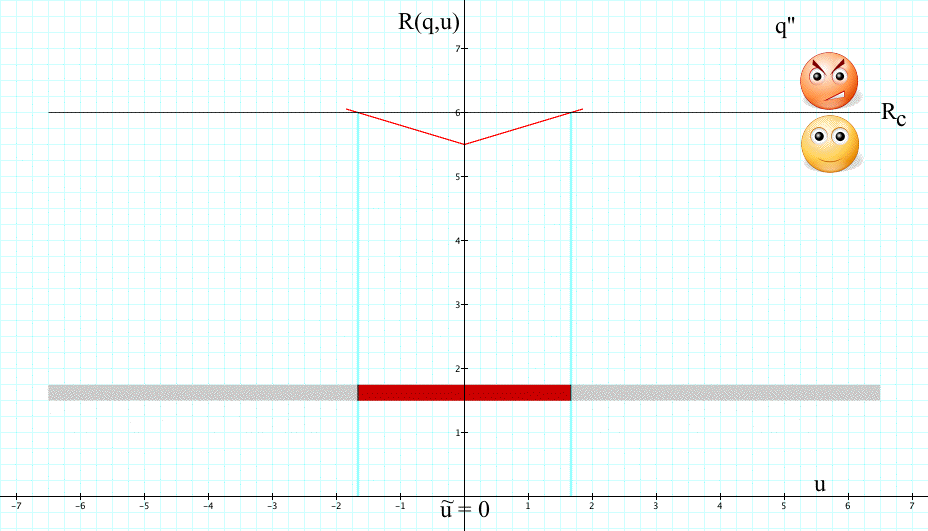
To see more clearly how absurd this idea really is, consider the performance of an alternative decision, call it q':

where R(q',u) continues its linear ascent in both directions over the interval U=[-7,7]. The performance requirement is then R(q',u) ≥ 0.

Clearly, q' outperforms q on U=[-7,7] in the sense that R(q',u) > R(q,u) almost everywhere on U=[-7,7], except for two small intervals. Furthermore, R(q',u)> 0 almost everywhere on U whereas q violates the constraint R(q,u) > 0 on large sub-intervals of U.

But according to Info-Gap decision theory, q' is less robust then q.

And what is more, suppose that the uncertainty space is the entire real line rather than the bounded interval [-7,7], with the estimate û retaining its value, namely û = 3.

This major change in the uncertainty space has no impact whatsoever on the results generated by Info-Gap decision theory: q is still regarded as more robust than q'.

All that is left to say then is that this idea is so blatantly unscientific that there surely must be some scientific device available that refutes it outright.

Garbage In — Garbage Out Axiom

One of the precepts of sound scientific reasoning that staves off simplistic, misguided, proposals to solve difficult problems by disregarding that which makes them difficult to solve, is called the Garbage In Garbage Out (GIGO) Axiom.

In the case of modeling, it can be described as follows:

Garbage In   -----> Model ----->   Garbage Out

However, more relevant to our discussion is one of its many corollaries:

Corollary of the GIGO Axiom:

The results of an analysis are only as good as the estimates on which the analysis is based.

The above outright rejection of the local approach to robustness against severe uncertainty of the type addressed by Info-Gap decision theory is based on this universally accepted precept. Since under severe uncertainty the estimate û is a wild guess, the results generated by a local robustness analysis that is conducted on a small neighborhood around this estimate — rather than on the entire uncertainty space U — would be treated as ... wild guesses as well.

The picture is this:

wild guess   ----->       Local Robustness Model      ----->   wild guess

In short, my advise is simple:

Moshe's Advice:

If someone is trying to sell you the idea — even from the pages of prestigious scientific journals — that robustness against severe uncertainty can be achieved by a local analysis of a small neighborhood of a wild guess of the true value of the parameter of interest — run a mile!.

Treat any such theory as a voodoo decision theory.

By necessity, a proper treatment of severe uncertainty requires a global approach to robustness, meaning that the robustness analysis must be based on the entire uncertainty space U. The reason is simple: the lack of any measure of likelihood regarding the location of the true value of u in U prohibits discarding neighborhoods of U from the robustness analysis.

Back to Info-Gap decision theory.

Info-Gap Robustness

By definition, Info-Gap's robustness is a local robustness, more accurately, it is a robustness obtained in the neighborhood of a point estimate of the parameter of interest.

So the immediate important implication of this key point is that the robustness yielded by Info-Gap's analysis for a decision can be totally different from the global robustness that is determined relative to the entire uncertainty space under consideration.

To examine this point formally, consider the following uncertainty model deployed by Info-Gap decision theory:

Info-Gap Uncertainty model:

  • u = parameter of interest.

  • u* = true value of u (unknown and subject to severe uncertainty)

  • û = estimate of u*.

  • U(α,û) = region of uncertainty of size α around û. These sets are assumed to be nested:

    • U(0,û) = {û}

    • U(α,û) ⊆ U(α+ε,û), for all α,ε ≥0

  • U = uncertainty space (a set containing U(α,û), for all û ≥ 0)

Note that the uncertainty space U is allowed to be unbounded.

Another key point to keep in mind is that the robustness sought by Info-gap's analysis is with respect to the satisfaction of a performance requirement (constraint).

Info-Gap performance model:

So, the guiding idea driving this analysis is to identify a decision that performs well — with respect to the performance requirement — on the uncertainty space U.

To enable a good appreciation of how flawed Info-gap's approach to obtaining robustness against severe uncertainty is, we shall set it off against a sound/logical approach which, unlike Info-Gap, takes full account of the central difficulty posed by severe uncertainty: our ignorance of the true value u. So, looking at the situation confronting us we would reason along the following lines.

In an ideal world we would have obtained a decision q* in Q such that the performance requirement R(q*,u) ≤ Rc is satisfied for all u in U. Such decisions would have been deemed super-robust. But, as we do not inhabit an ideal world, in our world such decisions rarely exist. Indeed, typically, no decision in Q is super-robust.

So, as a rule, we need to lower our expectations and settle instead for a decision q' in Q such that the performance requirement R(q',u) ≤ Rc is satisficed over a large subset of U. The merit of this proposition is that it enables regarding the "size" of this subset as a "measure" of the robustness of decision q'.

In other words, adopting this line allows defining the robustness of decision q as the size of the largest subset of U over which the performance requirement R(q,u) ≤ Rc is satisfied (for all u in that subset). Still, for this definition to be rigorous, we need to come up with a definition to measure the size of subsets of U. So, consider the following: let ρ(V) denote the size of a subset V of U, in which case we can define the robustness of decision q as follows:

Definition:

Global Robustness of decision q∈Q:     ρ*(q):= max     ρ(V)    
V⊆U
R(q,u)≤Rc,∀u∈V

So far so good, except that....

This is not the way robustness is defined by Info-Gap decision theory. To wit:

Definition:

Info-Gap Robustness of decision q∈Q:     α(q,û):=   max   {α≥0: R(q,u) ≤ Rc , ∀u∈U(α,û)}

Optimal Info-Gap Robustness:     α(û):=   max
q∈Q 		  α(q,û)
 
=   max
q∈Q		   max   {α≥0: R(q,u) ≤ Rc , ∀u∈U(α,û)}

In other words, when evaluating the robustness of decision q, Info-Gap decision theory does not consider all the subsets of U over which q satisfices the performance requirement. It considers a far more limited class of subsets of U. Namely, only those subsets of the form specified by its regions of uncertainty U(α,û), α>0. All other subsets of U are ignored.

The optimal (maximal) robustness is the largest value of α(q,û) over the set of available decisions Q. Info-Gap decision theory selects then a decision q* ∈Q such that α(q*,û) ≥ α(q,û), for all q in Q.

Example 1

Consider the case where U is the two dimensional Euclidean space, û=(1,1), and

U(α,û)={u∈U: (u1 - û1)2 + 2(u2 - û2)2 ≤ α} , α≥ 0.

That is, a region of uncertainty of size α is the area contained in the ellipse (u1 - û1)2 + 2(u2 - û2)2 ≤ α.

Suppose that Q={q',q''} and that the feasible regions of the performance constraint R(q,u) ≤ Rc for the two decisions are as shown in the picture.

The largest region of uncertainty U(α,û) for decision q' is obtained by increasing the size of the ellipse until it touches the line R(q',u)=Rc, as shown in the picture (point a). Similarly, the largest region of uncertainty U(α,û) for decision q' is obtained by increasing the size of the ellipse until it touches the line R(q'',u)=Rc (point b). The corresponding values of α are, by definition, α(q',û) and α(q'',û), respectively.

Since α(q'',û) > α(q',û), Info-Gap decision theory declares q'' to be more robust than q'.

Conceptually, Info-Gap's evaluation of the robustness of decision q can be described as follows:

Evaluation of Info-Gap-Robustness of decision q:

  1. Start at the estimate û with α=0.

  2. Slowly increase the region of uncertainty U(α,û) by increasing the value of α.

  3. If R(q,u) ≤ Rc for all u in U(α,û), go to 2.

  4. Else, stop!

Observe that the immediate consequence of Info-Gap's regions of uncertainty being nested is that the analysis is completely oblivious to how well/poorly decision q performs outside the region U(α(q,û),û). It is patently clear, therefore, that there can be significant differences between the global robustness and the Info-Gap robustness of a decision.

Examples, please!

The objective of the examples discussed below is to illustrate Info-Gap's definition of robustness and to show why this definition is utterly unsuitable for decision-making under severe uncertainty.

In particular, the objective is to make vivid the failure of local robustness to cope with severe uncertainty.

Example 1:

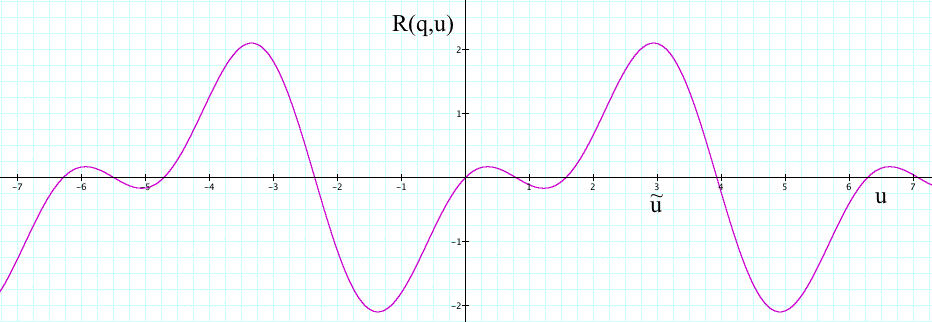
Consider the situation depicted in Figure 1:


Figure 1: Info-Gap Robustness of q'

and assume that U=(-∞,∞), and U(α,û):= {u: |u-û| ≤ α}. Since û = 0, we have U(α,û):= {u: |u| ≤ α}.

As indicated by the picture, the critical values of u are approximately 1.3 and -1.3, or equivalently α(q',û) ≈ 1.3.

But, it is clear that the picture indicates nothing about the global robustness of q'.

To be able to appreciate why this type of robustness cannot even be contemplated in decision under severe uncertainty, let us see what happens when we compare the robustness of two decisions. So, let us repeat the exercise with another decision.

Example 2:

Consider the situation depicted in Figure 2:


Figure 2: Info-Gap Robustness of q''

and as before, assume that U=(-∞,∞), and U(α,û):= {u: |u-û| ≤ α}. Since û = 0, we have U(α,û):= {u: |u| ≤ α}.

As indicated by the picture, the critical values of u are approximately 1.7 and -1.7, or equivalently that α(q'',û) ≈ 1.7.

But, it is clear that the picture indicates nothing about the global robustness of q''.

Let us now place the two cases in the same picture. This will bring out clearly the relationship between the performance of q' and that of q'':


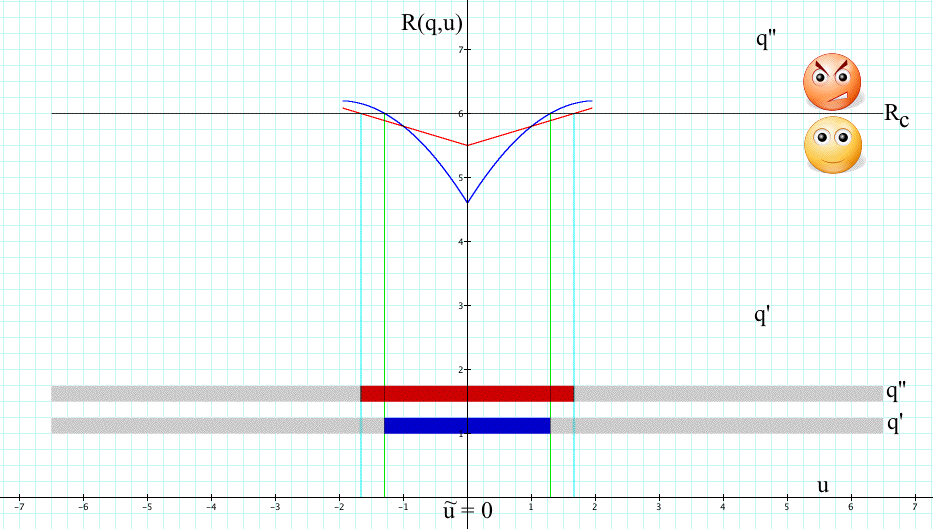
Figure 3: Info-Gap Robustness of q' and q''

The first assignment merely tests your vision:

Assignment # 1:

Rank the decisions q' and q'' according to their Info-Gap robustness. Explain the rationale for this ranking.

The second assignment tests your common sense and/or sense of humor (tick one):

Assignment # 2:

Rank the decisions q' and q'' according to their Global robustness. Explain the rationale for this ranking.

There are no official submission deadlines for these assignments. So take your time and feel free to consult your lecture notes, books, colleagues, neighbors, pets, etc.

But, please, avoid consulting the analysis below!

The Mother of All Examples

To bring out more forcefully the local nature of Info-Gap's robustness analysis, we now reveal more details about the performance of the decisions q' and q''. Keep in mind that the uncertainty space U (according to Info-Gap) is unbounded. This means of course that this picture is by necessity only a faint reflection of the real picture!

For simplicity assume that R(q',u) continues its quadratic decent (with respect to u) in both directions and that R(q'',u) continues its linear ascent (with respect to u) in both directions.

Assignment # 3:

Rank the decisions q' and q'' according to their Global and Info-Gap robustness. Explain the rationale for this ranking.

Use the animation facility at the bottom of the picture to simulate the Info-Gap robustness analysis. Read the commentary on your progress.

Notice Board

Welcome!

We are ready when you are!     Start!

The example below (my favorite) was inspired by a similar example that was created by my 2008 Honors student, Daphne Do, to illustrate the flaws in Info-Gap's robustness model.

Daphne's Example

Consider the case where the complete uncertainty space is a square of size 10 centered at the origin, the estimate is û=(-4,4) and the decision space is Q={q',q''}. Now suppose that we define regions of uncertainty such that U(α,û) is a circle of radius α centered at û. Next, suppose that q' satisfices the performance requirement on the square of size 2.2 shown by the shaded area in Figure 4(a) and that q'' satisfices the performance requirement on the rectange shown by the shaded area in Figure 4(b).

Robustness of q'     Robustness of q''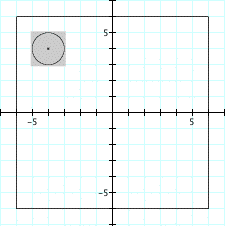
 
(a)     (b)
Figure 4. Info-Gap Robustness of q' and q''.

Info-Gap's robustness of q' is then α(q',û);=1.1 and for q'' we have α(q',û);=1. So Info-Gap decision theory therefore declares q' more robust than q''.

Assignment 4:

Write a short essay (no more than one page long) to address the following question: should you have to defend/justify your position (may be in court), which decision would you select as the more robust, q' or q''?

Your analysis should make explicit reference to the fact that the uncertainty is severe, namely that û is a wild guess, a poor indication of the true value of u and is likely to be substantially wrong.

And talking about Daphne, here is another example that was inspired by one of the examples in her honors thesis.

Daphne's other example

Suppose that the severe uncertainty under consideration is about a sick pixel of a large LCD screen, say a 2000x1000 (pixels) screen. Here it is:

We do not have a clue which pixel is the sick one, so ... we make a "wild guess" ... selecting the pixel in the middle of the screen.

Next, we need to decide what device to purchase for locating the sick pixel, as 2 such devices, call them "Green" and "Yellow" are available.

The following picture shows the capabilities of the "Yellow" device. That is, this device will be able to locate the sick pixel if the sick pixel is located in the marked yellow area of the screen.

The black dot in the middle of the screen is our wild guess of the sick pixel's location on the screen. The "true" location can be anywhere on the screen.

This picture illustrates the capabilities of the "Green" device.

The dashed gray circle represents the boundary of the "Yellow" circle. Clearly, the green circle is larger than the yellow circle.

Hence, according to Info-Gap decision theory, the "Green" device is more robust than the "Yellow" against the severe uncertainty in the sick pixel’s location on the screen.

Assignment 5:

Write a short essay (no more than one page long) to address the following question: should you have to defend/justify your decision (may be in court), which device will you select as the more robust, the "Yellow" or the "Green"?

Your analysis should make explicit reference to the fact that the uncertainty is severe, namely that the estimate is a wild guess, a poor indication of the true value, and is likely to be substantially wrong.

The Invariance Property

Info-Gap's robustness model exhibits a property that can be described by one term only: bizarre. Although it is designed to tackle severe uncertainty, the model takes no notice whatsoever of the severity of the uncertainty against which robustness is sought. That is, focusing all the while on the "safe" region of uncertainty U(α(û),û), the model generates the same results regardless of how large/small the uncertainty space actually is. Recall that α(û) denotes the robustness of the most robust decision.

Info-Gap's No Man's Land

  • The large rectangle represents the compete region of uncertainty, U.

  • α' is the robustness of some decision q, namely α' = α(q,û) for some q∈Q.

  • ε is some small positive constant.

  • So by definition, q satisfies the performance requirement at every point in U(α',û).

  • By definition, q violates the performance constraint at least in one point in U(α'+ε,û).

  • Hence, the area outside U(α'+ε,û) is a No Man's Land: the robustness of q is totally unaffected by how well/badly q performs outside U(α'+ε,û).

  • Therefore, if U(α+ε,û) is relatively much smaller than U, the robustness of q as determined by Info-Gap's robustness model, namely α', does not represent how well/badly q performs over the complete region of uncertainty U.

For example, in the context of the problem featured in Daphne's example, Info-Gap's robustness model will yield the same resutls, namely α(q',û);=1.1 and α(q',û);=1, for any uncertainty space U containing the circle of radius 1.1 + ε centered at û=(-4,4), where ε is any positive number (can be arbitrarily small), say 0.00001.

Doesn't this property in effect bring out the absurd in the claim that Info-Gap decision theory is designed specifically for the treatment of severe uncertainty and that its forte is in its ability to handle unbounded regions of uncertainty?

For what this theorem effectively reveals is that Info-Gap's secret weapon for handling an unbounded uncertainty space is simply to duck it. By localizing the analysis around the estimate û it simply takes no notice of how large/small the uncertainty space is!

The picture is this:

In this picture α' = α(û) + &epsilon for some (arbitrarily) small ε>0.

Note that the optimal decision and its robustness remain unchanged despite the complete region of uncertainty U growing from U' to U'', to U''' and so on.

All that is left to say is that only a theory that completely ignores the severity of the uncertainty under consideration can put forward a robustness model possessing such a bizarre property.

Clearly, this is absurd both methodologically and practically.

For consider, had it worked! We could have worked wonders, using Info-gap's "ignore it, mate!" recipe for severe uncertainty, to handle other complicated problems involving severe uncertainty!

But its complete debacle is made clear when it is realized that not only is Info-Gap decision theory incapable of dealing with Black Swans, it is even not equipped to deal with plain, ordinary, white swans.

A formal treatment of this property can be found at FAQs about Info-Gap.

On the brighter side, though, it is heartening that we can rely on the good old Garbage In Garbage Out Axiom and its many corollaries to guard against such fundamentally flawed theories.

The Maximin connection

Info-Gap decision theory is being promoted as a distinct, novel, revolutionary theory that is radically different from all theories for decision under uncertainty.

But is this fact or fiction?

It turns out that not only isn't Info-Gap's robustness model new, it is in fact a simple instance of the most well known robustness model in classical decision theory: Wald's Maximin model (circa 1940). Keep in mind though — as indicated above — that Info-Gap's implementation of this model is flawed because it is a local implementation.

A formal treatment of this Maximin/Info-Gap connection can be found at FAQs about Info-Gap.

How wrong can one be?

To see how far astray can the Info-Gap rhetoric lead unwary analysts, consider this.

The Info-Gap literature is spotted with contentions that Info-Gap's robustness analysis answers the folowing question:

Popular question: how wrong can our best guess be, and the contemplated decision still yields adequate results?

where "best guess" refers to the estimate û and "adequate results" means that the performance requirement is satisficed.

Of course, Info-Gap's robustness analysis does not address — much less can it answer — this question. Indeed, how could it? How can we possibly determine how wrong the estimate is if the true value is unknown?

Rather, by definition, Info-Gap's robustness analysis answer the following question:

Question: What is the largest value of α such that decision q satisfices the performance requirement for every u in U(α,û)?

If we agree that α represents a "deviation" from the estimate û and that a subset of U is safe if the performance requirement is satisfied at every u in the region, then the question can be phrased as follows:

Question: How much can we deviate from the estimate so that the region of uncertainty defined by this deviation is safe?

And if we agree that a safe region around û is a region of uncertainty U(α,û) for some value of α that is safe, then we can phrase the question thus:

Question: How large is the safe region around the estimate?

For example, consider the situation depicted in Figure 5, where the white areas represent subsets of U where the performance constraint is safisficed by the decision under consideration and the shaded areas represent regions of U where the decision violates the requirement and the circles represent the boundaties of regions of uncertainty of various sizes around the estimate.

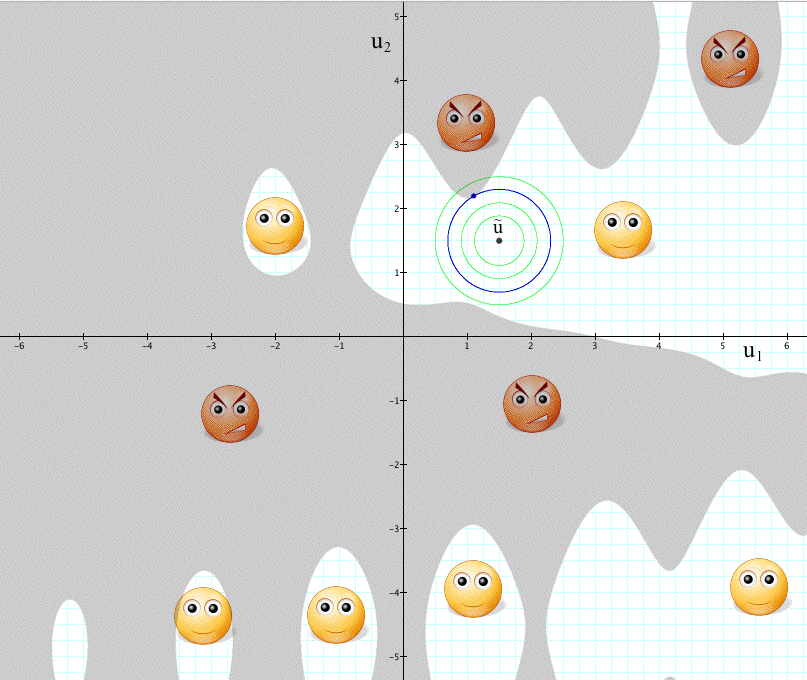
Figure 5: How wrong can I be What is the larget safe region around the estimate?

We have not the foggiest idea where the true value of u is. So, we cannot have the foggiest idea how wrong the estimate û is. Nor can we know how wrong a particular value of u in U is.

The thick blue circle represents the largest safe region of uncertainty around the estimate. This is yielded by the robustness model, together with the decision giving this particular safe circle.

Note that there can be values of u that are distant from û yet safe, and values of u that are very close to û yet unsafe. The local nature of Info-Gap's definition of robustness precludes this important property of the performance requirement.

In short, Info-Gap's robustness analysis instructs us on how robust we are in specific neighborhoods of the (the bad) estimate. But it tells us nothing about how robust we are with respect to the given uncertainty space U.

And a final word about the Invariance Property, note that the entire area outside the thick blue circle is a No Man's Land. This area is completely left out of Info-Gap's robustness analysis. Meaning that Info-Gap's robustness model is completely oblivious to the behavior of R(q,u) in this area.

Under the lamp post

As we have seen, Info-Gap’s prescription to conduct a local robustness analysis in the management of severe uncertainty is so manifestly flawed, that it is incomprehensible why Info-Gap scholars do not see this.

Having discussed this issue with a number of Info-Gap scholars, the following picture emerges.

Info-Gap scholars seem to be unaware of the contradiction between the following facts:

So when you ask them:

Q: How can a local analysis in the neighborhood of a wild guess possibly generate results that represent the performance of decisions over the complete given uncertainty space?

you get all sorts of interesting answers. These answers have one feature in common, they ... do not answer the question.

I'll mention three typical answers:

So, what can one say about this position except to remind those who invoke it in defense of an indefensible approach of the following. One does not even begin to address the difficulty posed by severe uncertainty by a priori confining the analysis to a neighborhood of a wild guess and then justify this as the "best approach" available under the circumstances. For, this is a typical "Lamp Post" approach to solving difficult problems:

The bright graduate student had gathered the appropriate author data. But when she encountered severe problems in performing the institutional part of the study (there was just no good way, using the standard library tools, to gather the necessary data) she simply ignored those problems and proceeded to accomplish what she could accomplish!

The result, of course, was fairly worthless. Solving the easy half of a problem while ignoring the more difficult half is simply not a problem solution. At the time it did not seem very funny; but in retrospect, this was the prototypical novice programmer’s mistake of solving the problem they wanted to solve and knew how to solve, rather than the problem the customer wanted solved!

Back in an era well before political correctness (during the 1940~1, there was a "little moron" series of jokes, and one of them went like this:

Person to little moron (PTLM: "What are you doing there under the lamp post?"
Little moron (LM): "Looking for my watch."
PTLM: "Where did you lose it?"
LM: "Over there."
PTLM: "If you lost it over there, why are you looking here under the lamp post?"
LM: "Because the light is better."

Using the easy solution is apparently a timehonored (if failed) approach!

Fortunately, those problems are well behind us.

Editor’s Corner
Top Scholars and Institutions Study Reaching Maturity: A Lesson Re-Learned
Robert L. Glass
Journal of Systems and Software
39(1), 1-2, 1997

Info-Gap scholars are advised that in most (all ?) countries there are no government regulations forbidding the exploration of the uncertainty space for the purpose of evaluating the global performance of decisions on this space. In the literature of "Robust Optimization" and "Robust Decision-Making" this is known as Scenario Generation.

The fact that the estimate we have is poor should spur us to explore the uncertainty space in areas that are distant from the estimate. Indeed, the more severe the uncertainty, the more important it is to carry out a global exploration of the uncertainty space.

Conclusions

To sum it all up:

It is patently clear that Info-Gap's local analysis cannot possibly be counted on to yield reliable results because its mode of operation flies in the face of the requirements of severe uncertainty.

Indeed, the incessant (inadvertently amusing) emphasis on Info-Gap's membership in the exclusive club of theories capable of handling unbounded uncertainty spaces in effect proves its undoing.

Because what this much vaunted ability effectively comes down to is that the unbounded uncertainty space is ignored altogether. That is, although an unbounded uncertainty space is postulated, the analysis is restricted to the locale of the (poor) estimate.

So, as pointed out above, methodologically this means that the severe uncertainty is ignored thus making a mockery of what decision-making in the face of severe uncertainty is all about.

If you have not done it already, this is the right time to browse through the following pages:

My personal advice to Info-Gap users is: remember the old saying

If it is too good to be true, it is!

Of course, by now most people — but certainly not all — correctly identify certain e-letters requesting details of your bank account so that the sum of $23,000,000 could be deposited in it — for what they are: too good to be true. Here is an example of a letter I received yesterday:

Date: Sat, 6 Jun 2009 08:24:23 -0400
To: undisclosed-recipients:
From: mr  ?????????? 
Reply-to: ????????? 
Subject: Good day,


Good day,

My name is Mr Jack Parkinson, I work with the UK Lottery. I am soliciting
your assistance for a swift transfer of 4,528,000 GBP, should you be
willing to assist me in this project, you will be giving me just 40% of
your winnings. Just as a brief, due to my position in the company I can
make it happen that you would be a winner of the above stated
amount.

   Naturally, every body would like to play a lottery if they are assured of
winning. I am assuring you today to be a winner, please do not take for
granted this once in a life time opportunity as we both stand to
collectively gain from this at the success of the transaction. Should you
be willing to assist me in this transaction please do respond to my
secure e-mail: ??????????


Regards,
Mr ?????????

But you still hear of tragic cases where someone actually took the bite.

So is there a remedy to guard against the "too good to be true" phenomenon?

Consider this with regard to gimmicks, gadgets and fad diets:

Sounds too good to be true?

If it sounds too good to be true, it probably is! There is no 'magic' diet that will achieve miraculous weight loss with very little effort and there is no 'magic' pill or potion that will melt fat away. When considering a weight loss program use your common sense and judgment and investigate the weight loss program or approach by asking lots of questions, like those listed in 'Ten questions to ask about weight loss programs'.

www.nestle.com.au/Nutrition/Shape/WeightLossApproach/TooGoodToBeTrue.htm (downloaded on June 6, 2009)

The Info-Gap experience has shown that the "too good to be true" adage also applies to science, notably publications in refereed scientific journals.

So what "common sense" questions should we come up with to expose the "too good to be true" element in Info-Gap decision theory?

I suggest that the following short list can be a good starting point:

  1. How can a local analysis in the neighborhood of a wild guess possibly guarantee that the decisions it generate are robust against severe uncertainty without violating the Garbage In — Garbage Out Axiom?

  2. Isn't it the case that the fundamental difficulty associated with decision-making under severe uncertainty is precisely the fact that we do not expect a local analysis in the neighborhood of a wild guess to yield decisions that are robust against severe uncertainty?

  3. Doesn't Info-Gap decision theory violate the universally accepted assumption that the results generated by a model can be only as good as the estimates on which the model is based?

  4. Given that Info-Gap's robustness model clearly cannot handle Black Swans and that Black Swans are often associated with severe uncertainty, what is the basis for the assertion that Info-Gap decision theory is designed specifically for decision-making in the face of severe uncertainty?

  5. In what way, if any, will the local Info-Gap robustness analysis change if we know that the uncertainty is not severe and that the estimate is good?

Stay tuned ... there is more in store ....

Welcome to Factland

This contribution is dedicated to the Info-Gap people at Wikipedia. They were searching for a formal proof that ....

 

Fact 1: Info-Gap is a simple instance of Wald's Maximin model [circa 1940].

 

Fact 2: Info-Gap does not deal with severe uncertainty: it simply ignores it.

Recent Articles, Working Papers, Notes

Also, see my complete list of articles
    Moshe's new book!
  • Sniedovich, M. (2012) Fooled by local robustness, Risk Analysis, in press.

  • Sniedovich, M. (2012) Black swans, new Nostradamuses, voodoo decision theories and the science of decision-making in the face of severe uncertainty, International Transactions in Operational Research, in press.

  • Sniedovich, M. (2011) A classic decision theoretic perspective on worst-case analysis, Applications of Mathematics, 56(5), 499-509.

  • Sniedovich, M. (2011) Dynamic programming: introductory concepts, in Wiley Encyclopedia of Operations Research and Management Science (EORMS), Wiley.

  • Caserta, M., Voss, S., Sniedovich, M. (2011) Applying the corridor method to a blocks relocation problem, OR Spectrum, 33(4), 815-929, 2011.

  • Sniedovich, M. (2011) Dynamic Programming: Foundations and Principles, Second Edition, Taylor & Francis.

  • Sniedovich, M. (2010) A bird's view of Info-Gap decision theory, Journal of Risk Finance, 11(3), 268-283.

  • Sniedovich M. (2009) Modeling of robustness against severe uncertainty, pp. 33- 42, Proceedings of the 10th International Symposium on Operational Research, SOR'09, Nova Gorica, Slovenia, September 23-25, 2009.

  • Sniedovich M. (2009) A Critique of Info-Gap Robustness Model. In: Martorell et al. (eds), Safety, Reliability and Risk Analysis: Theory, Methods and Applications, pp. 2071-2079, Taylor and Francis Group, London.
    • .
  • Sniedovich M. (2009) A Classical Decision Theoretic Perspective on Worst-Case Analysis, Working Paper No. MS-03-09, Department of Mathematics and Statistics, The University of Melbourne.(PDF File)

  • Caserta, M., Voss, S., Sniedovich, M. (2008) The corridor method - A general solution concept with application to the blocks relocation problem. In: A. Bruzzone, F. Longo, Y. Merkuriev, G. Mirabelli and M.A. Piera (eds.), 11th International Workshop on Harbour, Maritime and Multimodal Logistics Modeling and Simulation, DIPTEM, Genova, 89-94.

  • Sniedovich, M. (2008) FAQS about Info-Gap Decision Theory, Working Paper No. MS-12-08, Department of Mathematics and Statistics, The University of Melbourne, (PDF File)

  • Sniedovich, M. (2008) A Call for the Reassessment of the Use and Promotion of Info-Gap Decision Theory in Australia (PDF File)

  • Sniedovich, M. (2008) Info-Gap decision theory and the small applied world of environmental decision-making, Working Paper No. MS-11-08
    This is a response to comments made by Mark Burgman on my criticism of Info-Gap (PDF file )

  • Sniedovich, M. (2008) A call for the reassessment of Info-Gap decision theory, Decision Point, 24, 10.

  • Sniedovich, M. (2008) From Shakespeare to Wald: modeling wors-case analysis in the face of severe uncertainty, Decision Point, 22, 8-9.

  • Sniedovich, M. (2008) Wald's Maximin model: a treasure in disguise!, Journal of Risk Finance, 9(3), 287-291.

  • Sniedovich, M. (2008) Anatomy of a Misguided Maximin formulation of Info-Gap's Robustness Model (PDF File)
    In this paper I explain, again, the misconceptions that Info-Gap proponents seem to have regarding the relationship between Info-Gap's robustness model and Wald's Maximin model.

  • Sniedovich. M. (2008) The Mighty Maximin! (PDF File)
    This paper is dedicated to the modeling aspects of Maximin and robust optimization.

  • Sniedovich, M. (2007) The art and science of modeling decision-making under severe uncertainty, Decision Making in Manufacturing and Services, 1-2, 111-136. (PDF File) .

  • Sniedovich, M. (2007) Crystal-Clear Answers to Two FAQs about Info-Gap (PDF File)
    In this paper I examine the two fundamental flaws in Info-Gap decision theory, and the flawed attempts to shrug off my criticism of Info-Gap decision theory.

  • My reply (PDF File) to Ben-Haim's response to one of my papers. (April 22, 2007)

    This is an exciting development!

    • Ben-Haim's response confirms my assessment of Info-Gap. It is clear that Info-Gap is fundamentally flawed and therefore unsuitable for decision-making under severe uncertainty.

    • Ben-Haim is not familiar with the fundamental concept point estimate. He does not realize that a function can be a point estimate of another function.

      So when you read my papers make sure that you do not misinterpret the notion point estimate. The phrase "A is a point estimate of B" simply means that A is an element of the same topological space that B belongs to. Thus, if B is say a probability density function and A is a point estimate of B, then A is a probability density function belonging to the same (assumed) set (family) of probability density functions.

      Ben-Haim mistakenly assumes that a point estimate is a point in a Euclidean space and therefore a point estimate cannot be say a function. This is incredible!


  • A formal proof that Info-Gap is Wald's Maximin Principle in disguise. (December 31, 2006)
    This is a very short article entitled Eureka! Info-Gap is Worst Case (maximin) in Disguise! (PDF File)
    It shows that Info-Gap is not a new theory but rather a simple instance of Wald's famous Maximin Principle dating back to 1945, which in turn goes back to von Neumann's work on Maximin problems in the context of Game Theory (1928).

  • A proof that Info-Gap's uncertainty model is fundamentally flawed. (December 31, 2006)
    This is a very short article entitled The Fundamental Flaw in Info-Gap's Uncertainty Model (PDF File) .
    It shows that because Info-Gap deploys a single point estimate under severe uncertainty, there is no reason to believe that the solutions it generates are likely to be robust.

  • A math-free explanation of the flaw in Info-Gap. ( December 31, 2006)
    This is a very short article entitled The GAP in Info-Gap (PDF File) .
    It is a math-free version of the paper above. Read it if you are allergic to math.

  • A long essay entitled What's Wrong with Info-Gap? An Operations Research Perspective (PDF File) (December 31, 2006).
    This is a paper that I presented at the ASOR Recent Advances in Operations Research (PDF File) mini-conference (December 1, 2006, Melbourne, Australia).

Recent Lectures, Seminars, Presentations

If your organization is promoting Info-Gap, I suggest that you invite me for a seminar at your place. I promise to deliver a lively, informative, entertaining and convincing presentation explaining why it is not a good idea to use — let alone promote — Info-Gap as a decision-making tool.

Here is a list of relevant lectures/seminars on this topic that I gave in the last two years.

Disclaimer: This page, its contents and style, are the responsibility of the author (Moshe Sniedovich) and do not represent the views, policies or opinions of the organizations he is associated/affiliated with.


Last modified: